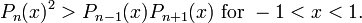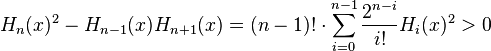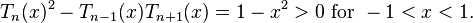Turán's inequalities

In mathematics, Turán's inequalities are some inequalities for Legendre polynomials found by Paul Turán (1950) (and first published by Szegö (1948)). There are many generalizations to other polynomials, often called Turán's inequalities, given by (E. F. Beckenbach, W. Seidel & Otto Szász 1951) and other authors.

If P_n is the nth Legendre polynomial, Turán's inequalities state that

\,\! P_n(x)^2 > P_{n-1}(x)P_{n+1}(x)\text{ for }-1<x<1.

For H_n, the nth Hermite polynomial, Turán's inequality is

H_n(x)^2 - H_{n-1}(x)H_{n+1}(x)= (n-1)!\cdot \sum_{i=0}^{n-1}\frac{2^{n-i}}{i!}H_i(x)^2>0

and for Chebyshev polynomials it is

\! T_n(x)^2 - T_{n-1}(x)T_{n+1}(x)= 1-x^2>0 \text{ for }-1<x<1.

References

Beckenbach, E. F.; Seidel, W.; Szász, Otto (1951), "Recurrent determinants of Legendre and of ultraspherical polynomials", Duke Math. J. 18: 1–10, MR 0040487
Szegö, G. (1948), "On an inequality of P. Turán concerning Legendre polynomials", Bull. Amer. Math. Soc. 54, 54 (4): 401–405, doi:10.1090/S0002-9904-1948-09017-6, MR 0023954
Turán, Paul (1950), "On the zeros of the polynomials of Legendre", Časopis Pěst. Mat. Fys. 75: 113–122, MR 0041284

Turán's inequalities

See also

References