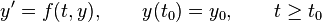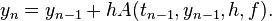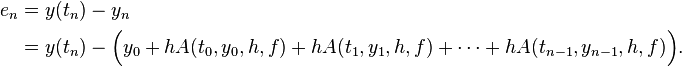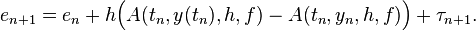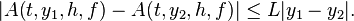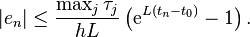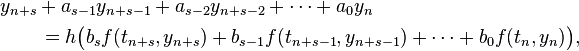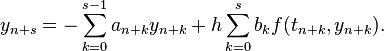Truncation error (numerical integration)
Truncation errors in numerical integration are of two kinds:
- local truncation errors – the error caused by one iteration, and
- global truncation errors – the cumulative error caused by many iterations.
Definitions
Suppose we have a continuous differential equation
and we wish to compute an approximation 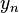 of the true solution
of the true solution 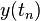 at discrete time steps
at discrete time steps  . For simplicity, assume the time steps are equally spaced:
. For simplicity, assume the time steps are equally spaced:
Suppose we compute the sequence 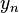 with a one-step method of the form
with a one-step method of the form
The function  is called the increment function, and can be interpreted as an estimate of the slope of
is called the increment function, and can be interpreted as an estimate of the slope of 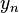 .
.
Local truncation error
The local truncation error 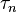 is the error that our increment function,
is the error that our increment function,  , causes during a single iteration, assuming perfect knowledge of the true solution at the previous iteration.
, causes during a single iteration, assuming perfect knowledge of the true solution at the previous iteration.
More formally, the local truncation error, 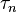 , at step
, at step  is computed from the difference between the left- and the right-hand side of the equation for the increment
is computed from the difference between the left- and the right-hand side of the equation for the increment 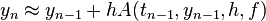 :
:
The numerical method is consistent if the local truncation error is 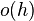 (this means that for every
(this means that for every 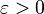 there exists an
there exists an  such that
such that 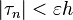 for all
for all 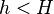 ; see big O notation). If the increment function
; see big O notation). If the increment function  is differentiable, then the method is consistent if, and only if,
is differentiable, then the method is consistent if, and only if, 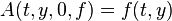 .[3]
.[3]
Furthermore, we say that the numerical method has order  if for any sufficiently smooth solution of the initial value problem, the local truncation error is
if for any sufficiently smooth solution of the initial value problem, the local truncation error is 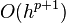 (meaning that there exist constants
(meaning that there exist constants  and
and  such that
such that 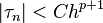 for all
for all 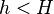 ).[4]
).[4]
Global truncation error
The global truncation error is the accumulation of the local truncation error over all of the iterations, assuming perfect knowledge of the true solution at the initial time step.
More formally, the global truncation error, 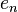 , at time
, at time 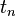 is defined by:
is defined by:
The numerical method is convergent if global truncation error goes to zero as the step size goes to zero; in other words, the numerical solution converges to the exact solution: 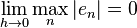 .[6]
.[6]
Relationship between local and global truncation errors
Sometimes it is possible to calculate an upper bound on the global truncation error, if we already know the local truncation error. This requires our increment function be sufficiently well-behaved.
The global truncation error satisfies the recurrence relation:
This follows immediately from the definitions. Now assume that the increment function is Lipschitz continuous in the second argument, that is, there exists a constant  such that for all
such that for all  and
and 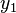 and
and 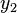 , we have:
, we have:
Then the global error satisfies the bound
It follows from the above bound for the global error that if the function  in the differential equation is continuous in the first argument and Lipschitz continuous in the second argument (the condition from the Picard–Lindelöf theorem), and the increment function
in the differential equation is continuous in the first argument and Lipschitz continuous in the second argument (the condition from the Picard–Lindelöf theorem), and the increment function  is continuous in all arguments and Lipschitz continuous in the second argument, then the global error tends to zero as the step size
is continuous in all arguments and Lipschitz continuous in the second argument, then the global error tends to zero as the step size 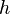 approaches zero (in other words, the numerical method converges to the exact solution).[8]
approaches zero (in other words, the numerical method converges to the exact solution).[8]
Extension to linear multistep methods
Now consider a linear multistep method, given by the formula
Thus, the next value for the numerical solution is computed according to
The next iterate of a linear multistep method depends on the previous s iterates. Thus, in the definition for the local truncation error, it is now assumed that the previous s iterates all correspond to the exact solution:
Again, the method is consistent if 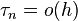 and it has order p if
and it has order p if 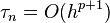 . The definition of the global truncation error is also unchanged.
. The definition of the global truncation error is also unchanged.
The relation between local and global truncation errors is slightly different from in the simpler setting of one-step methods. For linear multistep methods, an additional concept called zero-stability is needed to explain the relation between local and global truncation errors. Linear multistep methods that satisfy the condition of zero-stability have the same relation between local and global errors as one-step methods. In other words, if a linear multistep method is zero-stable and consistent, then it converges. And if a linear multistep method is zero-stable and has local error 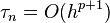 , then its global error satisfies
, then its global error satisfies 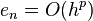 .[10]
.[10]
See also
- Order of accuracy
- Numerical integration
- Numerical ordinary differential equations
- Truncation error
Notes
- ↑ Gupta, G. K.; Sacks-Davis R.; Tischer P. E. (March 1985). "A review of recent developments in solving ODEs". Computing Surveys 17 (1): 5 – 47. doi:10.1145/4078.4079.
- ↑ Süli & Mayers 2003, p. 317, calls
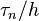 the truncation error.
the truncation error. - ↑ Süli & Mayers 2003, pp. 321 & 322
- ↑ Iserles 1996, p. 8; Süli & Mayers 2003, p. 323
- ↑ Süli & Mayers 2003, p. 317
- ↑ Iserles 1996, p. 5
- ↑ Süli & Mayers 2003, p. 318
- ↑ Süli & Mayers 2003, p. 322
- ↑ Süli & Mayers 2003, p. 337, uses a different definition, dividing this by essentially by h
- ↑ Süli & Mayers 2003, p. 340
References
- Iserles, Arieh (1996), A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press, ISBN 978-0-521-55655-2.
- Süli, Endre; Mayers, David (2003), An Introduction to Numerical Analysis, Cambridge University Press, ISBN 0521007941.