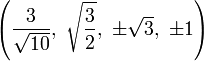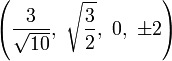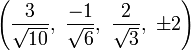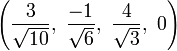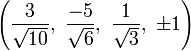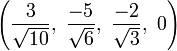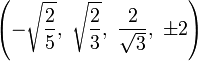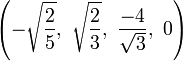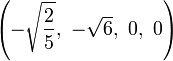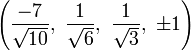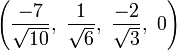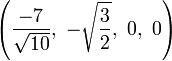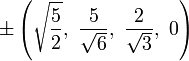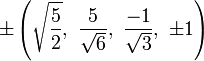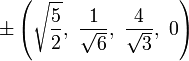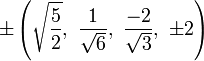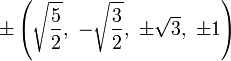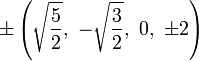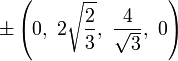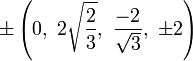Truncated 5-cell

5-cell	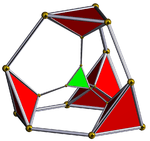Truncated 5-cell	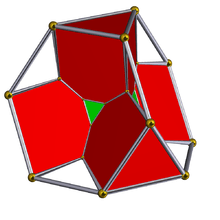Bitruncated 5-cell
Schlegel diagrams centered on [3,3] (cells at opposite at [3,3])

In geometry, a truncated 5-cell is a uniform 4-polytope (4-dimensional uniform polytope) formed as the truncation of the regular 5-cell.

There are two degrees of trunctions, including a bitruncation.

Truncated 5-cell

Truncated 5-cell
Schlegel diagram (tetrahedron cells visible)
Type	Uniform 4-polytope
Schläfli symbol	t_0,1{3,3,3}
Coxeter diagram
Cells	10	5 (3.3.3) 5 (3.6.6)
Faces	30	20 {3} 10 {6}
Edges	40
Vertices	20
Vertex figure	Irr. tetrahedron
Symmetry group	A₄, [3,3,3], order 120
Properties	convex, isogonal
Uniform index	2 3 4

The truncated 5-cell, truncated pentachoron or truncated 4-simplex is bounded by 10 cells: 5 tetrahedra, and 5 truncated tetrahedra. Each vertex is surrounded by 3 truncated tetrahedra and one tetrahedron; the vertex figure is an elongated tetrahedron.

Construction

The truncated 5-cell may be constructed from the 5-cell by truncating its vertices at 1/3 the edge length. This truncates the 5 tetrahedral cells into truncated tetrahedra, and introduces 5 new tetrahedral cells positioned on the original vertices.

Structure

The truncated tetrahedra are joined to each other at their hexagonal faces, and to the tetrahedra at their triangular faces.

Projections

The tetrahedron-first parallel projection of the truncated 5-cell into 3-dimensional space has the following structure:

The projection envelope is a truncated tetrahedron.
One of the truncated tetrahedral cells project onto the entire envelope.
One of the tetrahedral cells project onto a tetrahedron lying at the center of the envelope.
Four flattened tetrahedra are joined to the triangular faces of the envelope, and connected to the central tetrahedron via 4 radial edges. These are the images of the remaining 4 tetrahedral cells.
Between the central tetrahedron and the 4 hexagonal faces of the envelope are 4 irregular truncated tetrahedral volumes, which are the images of the 4 remaining trucated tetrahedral cells.

This layout of cells in projection is analogous to the layout of faces in the face-first projection of the truncated tetrahedron into 2-dimensional space. The truncated 5-cell is the 4-dimensional analogue of the truncated tetrahedron.

Images

orthographic projections
A_k Coxeter plane	A₄	A₃	A₂
Graph
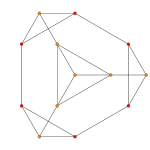Dihedral symmetry	[5]	[4]	[3]

net
stereographic projection
(centered on truncated tetrahedron)

Alternate names

Truncated pentatope
Truncated 4-simplex
Truncated pentachoron (Acronym: tip) (Jonathan Bowers)

Coordinates

The Cartesian coordinates for the vertices of an origin-centered truncated 5-cell having edge length 2 are:

\left( \frac{3}{\sqrt{10}},\ \sqrt{3 \over 2},\ \pm\sqrt{3},\ \pm1\right)

\left( \frac{3}{\sqrt{10}},\ \sqrt{3 \over 2},\ 0,\ \pm2\right)

\left( \frac{3}{\sqrt{10}},\ \frac{-1}{\sqrt{6}},\ \frac{2}{\sqrt{3}},\ \pm2\right)

\left( \frac{3}{\sqrt{10}},\ \frac{-1}{\sqrt{6}},\ \frac{4}{\sqrt{3}},\ 0 \right)

\left( \frac{3}{\sqrt{10}},\ \frac{-5}{\sqrt{6}},\ \frac{1}{\sqrt{3}},\ \pm1\right)

\left( \frac{3}{\sqrt{10}},\ \frac{-5}{\sqrt{6}},\ \frac{-2}{\sqrt{3}},\ 0 \right)

\left( -\sqrt{2 \over 5},\ \sqrt{2 \over 3},\ \frac{2}{\sqrt{3}},\ \pm2\right)

\left( -\sqrt{2 \over 5},\ \sqrt{2 \over 3},\ \frac{-4}{\sqrt{3}},\ 0 \right)

\left( -\sqrt{2 \over 5},\ -\sqrt{6},\ 0,\ 0 \right)

\left( \frac{-7}{\sqrt{10}},\ \frac{1}{\sqrt{6}},\ \frac{1}{\sqrt{3}},\ \pm1\right)

\left( \frac{-7}{\sqrt{10}},\ \frac{1}{\sqrt{6}},\ \frac{-2}{\sqrt{3}},\ 0 \right)

\left( \frac{-7}{\sqrt{10}},\ -\sqrt{3 \over 2},\ 0,\ 0 \right)

More simply, the vertices of the truncated 5-cell can be constructed on a hyperplane in 5-space as permutations of (0,0,0,1,2) or of (0,1,2,2,2). These coordinates come from positive orthant facets of the truncated pentacross and bitruncated penteract respectively.

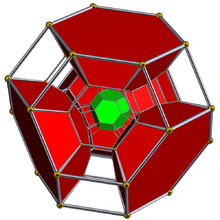
Bitruncated 5-cell

Schlegel diagram with alternate cells hidden.
Bitruncated 5-cell
Type	Uniform 4-polytope
Schläfli symbol	t_1,2{3,3,3}
Coxeter diagram	or
Cells	10 (3.6.6)
Faces	40	20 {3} 20 {6}
Edges	60
Vertices	30
Vertex figure	(Tetragonal disphenoid)
Symmetry group	Aut(A₄), [[3,3,3]], order 240
Properties	convex, isogonal isotoxal, isochoric
Uniform index	5 6 7

The bitruncated 5-cell (also called a bitruncated pentachoron, decachoron and 10-cell) is a 4-dimensional polytope, or 4-polytope, composed of 10 cells in the shape of truncated tetrahedra. Each hexagonal face of the truncated tetrahedra is joined in complementary orientation to the neighboring truncated tetrahedron. Each edge is shared by two hexagons and one triangle. Each vertex is surrounded by 4 truncated tetrahedral cells in a tetragonal disphenoid vertex figure.

The bitruncated 5-cell is the intersection of two pentachora in dual configuration. As such, it is also the intersection of a penteract with the hyperplane that bisects the penteract's long diagonal orthogonally. In this sense it is a 4-dimensional analog of the regular octahedron (intersection of regular tetrahedra in dual configuration / tesseract bisection on long diagonal) and the regular hexagon (equilateral triangles / cube). The 5-dimensional analog is the birectified 5-simplex, and the $n$ -dimensional analog is the polytope whose Coxeter–Dynkin diagram is linear with rings on the middle one or two nodes.

The bitruncated 5-cell is one of the two non-regular uniform 4-polytopes which are cell-transitive. The other is the bitruncated 24-cell, which is composed of 48 truncated cubes.

Symmetry

This 4-polytope has a higher extended pentachoric symmetry (2×A₄, [[3,3,3]]), doubled to order 240, because the element corresponding to any element of the underlying 5-cell can be exchanged with one of those corresponding to an element of its dual.

Alternative names

Bitruncated 5-cell (Norman W. Johnson)
10-cell as a cell-transitive 4-polytope
Bitruncated pentachoron
Bitruncated pentatope
Bitruncated 4-simplex
Decachoron (Acronym: deca) (Jonathan Bowers)

Images

orthographic projections
A_k Coxeter plane	A₄	A₃	A₂
Graph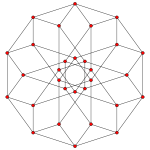
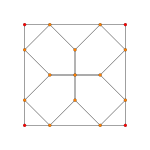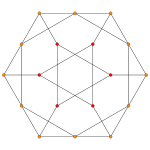Dihedral symmetry	[[5]] = [10]	[4]	[[3]] = [6]

stereographic projection of spherical 4-polytope (centred on a hexagon face)	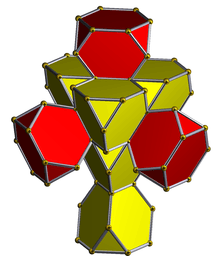Net (polytope)

Coordinates

The Cartesian coordinates of an origin-centered bitruncated 5-cell having edge length 2 are:

\pm\left(\sqrt{\frac{5}{2}},\ \frac{5}{\sqrt{6}},\ \frac{2}{\sqrt{3}},\ 0\right)

\pm\left(\sqrt{\frac{5}{2}},\ \frac{5}{\sqrt{6}},\ \frac{-1}{\sqrt{3}},\ \pm1\right)

\pm\left(\sqrt{\frac{5}{2}},\ \frac{1}{\sqrt{6}},\ \frac{4}{\sqrt{3}},\ 0\right)

\pm\left(\sqrt{\frac{5}{2}},\ \frac{1}{\sqrt{6}},\ \frac{-2}{\sqrt{3}},\ \pm2\right)

\pm\left(\sqrt{\frac{5}{2}},\ -\sqrt{\frac{3}{2}},\ \pm\sqrt{3},\ \pm1\right)

\pm\left(\sqrt{\frac{5}{2}},\ -\sqrt{\frac{3}{2}},\ 0,\ \pm2\right)

\pm\left(0,\ 2\sqrt{\frac{2}{3}},\ \frac{4}{\sqrt{3}},\ 0\right)

\pm\left(0,\ 2\sqrt{\frac{2}{3}},\ \frac{-2}{\sqrt{3}},\ \pm2\right)

More simply, the vertices of the bitruncated 5-cell can be constructed on a hyperplane in 5-space as permutations of (0,0,1,2,2). These represent positive orthant facets of the bitruncated pentacross.

Another 5-space construction are all 20 permutations of (1,0,0,0,-1).

Related polytopes

Isotopic uniform truncated simplices
Dim.	2	3	4	5	6	7	8
Name	t{3} Hexagon	r{3,3} Octahedron	2t{3,3,3} Decachoron	2r{3,3,3,3} Dodecateron	3t{3,3,3,3,3} Tetradecapeton	3r{3,3,3,3,3,3} Hexadecaexon	4t{3,3,3,3,3,3,3} Octadecazetton
Coxeter diagram
Images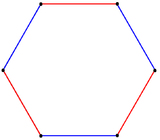
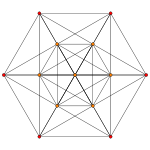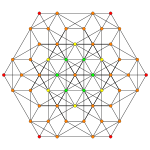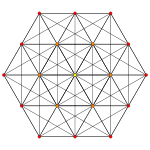Facets		{3}	t{3,3}	r{3,3,3}	2t{3,3,3,3}	2r{3,3,3,3,3}	3t{3,3,3,3,3,3}

Related regular skew polyhedron

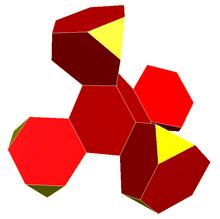
3}, with pairs of yellow triangles folded together into 4D and removed

The regular skew polyhedron, {6,4|3}, exists in 4-space with 4 hexagonal around each vertex, in a zig-zagging nonplanar vertex figure. These hexagonal faces can be seen on the bitruncated 5-cell, using all 60 edges and 20 vertices. The 20 triangular faces of the bitruncated 5-cell can be seen as removed. The dual regular skew polyhedron, {4,6|3}, is similarly related to the square faces of the runcinated 5-cell.

Related polytopes

These polytope are from a set of 9 uniform 4-polytope constructed from the [3,3,3] Coxeter group.

Name	5-cell	truncated 5-cell	rectified 5-cell	cantellated 5-cell	bitruncated 5-cell	cantitruncated 5-cell	runcinated 5-cell	runcitruncated 5-cell	omnitruncated 5-cell
Schläfli symbol	{3,3,3} 3r{3,3,3}	t{3,3,3} 2t{3,3,3}	r{3,3,3} 2r{3,3,3}	rr{3,3,3} r2r{3,3,3}	2t{3,3,3}	tr{3,3,3} t2r{3,3,3}	t_0,3{3,3,3}	t_0,1,3{3,3,3} t_0,2,3{3,3,3}	t_0,1,2,3{3,3,3}
Coxeter diagram
Schlegel diagram
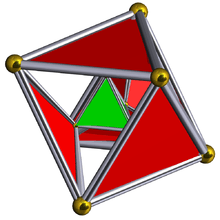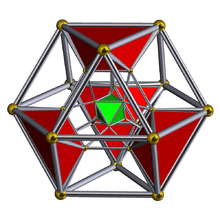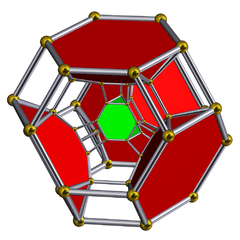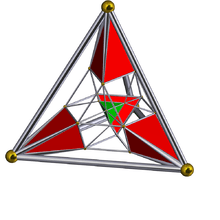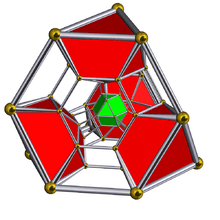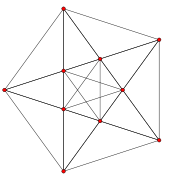
A₄ Coxeter plane Graph
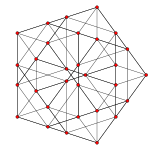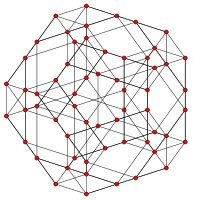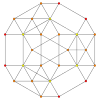
A₃ Coxeter plane Graph
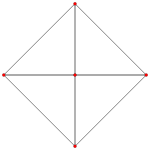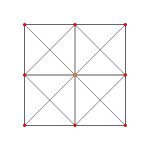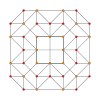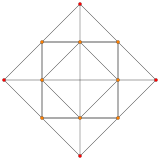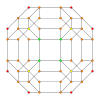A₂ Coxeter plane Graph

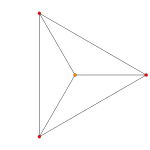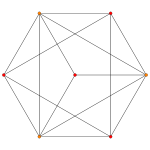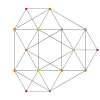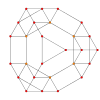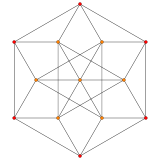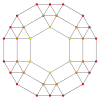References

H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  - (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  - (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 p.88 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
Olshevsky, George, Pentachoron at Glossary for Hyperspace.
- 1. Convex uniform polychora based on the pentachoron - Model 3, George Olshevsky.
Richard Klitzing, 4D, uniform polytopes (polychora) x3x3o3o - tip, o3x3x3o - deca

Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform 4-polytope	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes