Triple product property

In abstract algebra, the triple product property is an identity satisfied in some groups.

Let $G$ be a non-trivial group. Three nonempty subsets $S, T, U \subset G$ are said to have the triple product property in $G$ if for all elements $s, s' \in S$ , $t, t' \in T$ , $u, u' \in U$ it is the case that

s's^{-1}t't^{-1}u'u^{-1} = 1 \Rightarrow s' = s, t' = t, u' = u

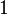where $1$ is the identity of $G$ .

It plays a role in research of fast matrix multiplication algorithms.

References

Henry Cohn, Chris Umans. A Group-theoretic Approach to Fast Matrix Multiplication. arXiv:math.GR/0307321. Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science, 11–14 October 2003, Cambridge, MA, IEEE Computer Society, pp. 438–449.