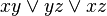Triple modular redundancy
In computing, triple modular redundancy, sometimes called triple-mode redundancy,[1] (TMR) is a fault-tolerant form of N-modular redundancy, in which three systems perform a process and that result is processed by a majority-voting system to produce a single output. If any one of the three systems fails, the other two systems can correct and mask the fault.
The TMR concept can be applied to many forms of redundancy, such as software redundancy in the form of N-version programming, and is commonly found in fault-tolerant computer systems.
Some ECC memory uses triple modular redundancy hardware (rather than the more common Hamming code), because triple modular redundancy hardware is faster than Hamming error correction software.[2] Space satellite systems often use TMR,[3] [4][5] although satellite RAM usually uses Hamming error correction.[6]
Some communication systems use N-modular redundancy as a simple form of forward error correction. For example, 5-modular redundancy communication systems (such as FlexRay) use the majority of 5 samples – if any 2 of the 5 results are erroneous, the other 3 results can correct and mask the fault.
Modular redundancy is a basic concept, dating to antiquity, while the first use of TMR in a computer was the Czechoslovak computer SAPO, in the 1950s.
Chronometers
To utilize triple modular redundancy, a ship must have at least three chronometers; with only two chronometers (dual modular redundancy), error detection is possible, but error correction is not. There is an old adage to this effect, stating: "Never go to sea with two chronometers; take one or three."[7] Meaning, if two chronometers contradict, how do you know which one is correct? At one time, the cost of three sufficiently accurate chronometers was more than the cost of a smaller merchant vessel.[8] Some vessels carried more than three chronometers – for example, the HMS Beagle carried 22 chronometers.[9]
The majority gate
In TMR, three identical logic circuits (logic gates) are used to compute the same set of specified Boolean function. If there are no circuit failures, the outputs of the three circuits are identical. But due to circuit failures, the outputs of the three circuits may be different. A majority gate is used to decide which of the circuits’ outputs is the correct output. The majority gate output is 1 if two or more of the inputs of the majority gate are 1; output is 0 if two or more of the majority gate’s inputs are 0. The majority gate is a simple AND–OR circuit: if the inputs to the majority gate are denoted by x, y and z, then the output of the majority gate is
Thus, the majority gate is the carry output of a full adder, i.e., the majority gate is a voting machine.[10]
TMR operation
Assuming the Boolean function computed by the three identical logic gates has value 1, then: (a) if no circuit has failed, all three circuits produce an output of value 1, and the majority gate output has value 1. (b) if one circuit fails and produces an output of 0, while the other two are working correctly and produce an output of 1, the majority gate output is 1, i.e., it still has the correct value. And similarly for the case when the Boolean function computed by the three identical circuits has value 0. Thus, the majority gate output is guaranteed to be correct as long as no more than one of the three identical logic circuits has failed.[10]
TMR systems should use data scrubbing—rewrite flip-flops periodically—in order to avoid accumulation of errors.[11]
The voter
The majority gate itself could fail. Is there a way to mask that failure? In other words, Who guards the guardians?[12]
In a few TMR systems, such as the Saturn Launch Vehicle Digital Computer and functional triple modular redundancy (FTMR) systems, the voters are also triplicated. Three voters are used – one for each copy of the next stage of TMR logic. In such systems there is no single point of failure. [13][14]
However, in contrast to the relatively complicated Boolean functions computed in triplicate by the TMR system, the majority gate is a simple circuit, thus its probability of failure is significantly smaller than that of each of the three circuits computing the Boolean function.[10] In other systems there is only a single voter—If the voter fails in such a system, then the complete system will fail. However, in a good TMR system the voter is much more reliable than the other TMR components.
Triple modular redundancy in popular culture
- The three pre-cogs in Minority Report lead to a conviction, even when one is in the minority.
- To rule out that a single win was "a fluke", some competitions use a two out of three falls match. This isn't true TMR, however, because the three falls are not independent of each other – each competitor knows who has most falls at any point in the competition, which influences their future actions.
- In Arthur C. Clarke's science fiction novel Rendezvous with Rama, the Ramans make heavy use of triple redundancy.
See also
- Fault tolerant system
- Dual modular redundancy
- Repetition code
- Lockstep (computing)
External links
- Article about TMR with reference to TMR usage in avionics and industry
- Johnson, J. M., & Wirthlin, M. J. (2010, February). Voter insertion algorithms for FPGA designs using triple modular redundancy. In Proceedings of the 18th annual ACM/SIGDA international symposium on Field programmable gate arrays (pp. 249–258). ACM.
References
- ↑ David Ratter. "FPGAs on Mars"
- ↑ "Using StrongArm SA-1110 in the On-Board Computer of Nanosatellite". Tsinghua Space Center, Tsinghua University, Beijing. Retrieved 2009-02-16.
- ↑ "Actel engineers use triple-module redundancy in new rad-hard FPGA". Military & Aerospace Electronics. Retrieved 2009-02-16.
- ↑ SEU Hardening of Field Programmable Gate Arrays (FPGAs) For Space Applications and Device Characterization
- ↑ FPGAs in Space
- ↑ Commercial Microelectronics Technologies for Applications in the Satellite Radiation Environment
- ↑ Brooks, Frederick J. (1995) [1975]. The Mythical Man-Month. Addison-Wesley. p. 64. ISBN 0-201-83595-9.
- ↑ "Re: Longitude as a Romance". Irbs.com, Navigation mailing list. 2001-07-12. Retrieved 2009-02-16.
- ↑ R. Fitzroy. "Volume II: Proceedings of the Second Expedition". p. 18.
- ↑ 10.0 10.1 10.2 Professor Dilip V. Sarwate, Lecture Notes for ECE 413 - Probability with Engineering Applications, Department of Electrical and Computer Engineering (ECE), UIUC College of Engineering, University of Illinois at Urbana-Champaign
- ↑ Wojciech M. Zabolotny et al. "Radiation tolerant design of RLBCS system for RPC detector in LHC experiment". Proceedings of SPIE. 2005.
- ↑ A.W. Krings. "Redundancy". 2007.
- ↑ Sandi Habinc. "Functional Triple Modular Redundancy (FTMR): VHDL Design Methodology for Redundancy in Combinatorial and Sequential Logic". 2002.
- ↑ R. E. Lyons and W. Vanderkulk. "The Use of Triple-Modular Redundancy to Improve Computer Reliability". IBM Journal. 1962.