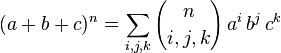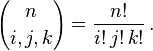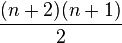Trinomial expansion

In mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomials. The expansion is given by

(a+b+c)^n = \sum_{i,j,k} {n \choose i,j,k}\, a^i \, b^j \, c^k

where n is a nonnegative integer and the sum is taken over all combinations of nonnegative indices i, j, and k such that i + j + k = n. The trinomial coefficients are given by

{n \choose i,j,k} = \frac{n!}{i!\,j!\,k!} \,.

This formula is a special case of the multinomial formula for m = 3. The coefficients can be defined with a generalization of Pascal's triangle to three dimensions, called Pascal's pyramid or Pascal's tetrahedron.

The number of terms of an expanded trinomial is

\frac{(n+2)(n+1)}{2}

where n is the exponent to which the trinomial is raised.

See also