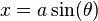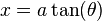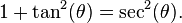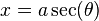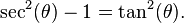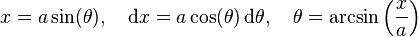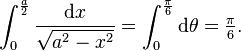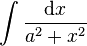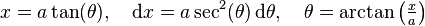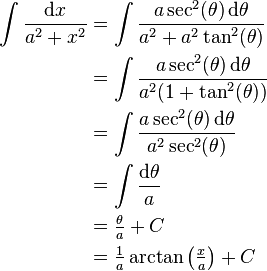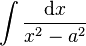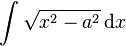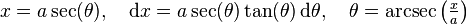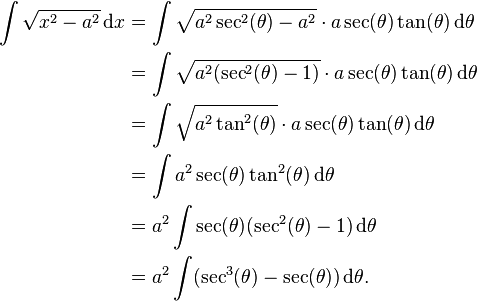Trigonometric substitution

Wikiversity has learning materials about Trigonometric Substitutions
Wikibooks has a book on the topic of: Calculus/Integration techniques/Trigonometric Substitution

In mathematics, Trigonometric substitution is the substitution of trigonometric functions for other expressions. One may use the trigonometric identities to simplify certain integrals containing radical expressions:[1][2]

Substitution 1. If the integrand contains a2 − x2, let
x = a \sin(\theta)

and use the identity

1-\sin^2(\theta) = \cos^2(\theta).
Substitution 2. If the integrand contains a2 + x2, let
x = a \tan(\theta)

and use the identity

1+\tan^2(\theta) = \sec^2(\theta).
Substitution 3. If the integrand contains x2 − a2, let
x = a \sec(\theta)

and use the identity

\sec^2(\theta)-1 = \tan^2(\theta).

Examples

Integrals containing a2 − x2

In the integral

\int\frac{\mathrm dx}{\sqrt{a^2-x^2}}

we may use

x=a\sin(\theta),\quad \mathrm dx=a\cos(\theta)\,\mathrm d\theta, \quad \theta=\arcsin\left(\frac{x}{a}\right)
\begin{align} \int\frac{\mathrm dx}{\sqrt{a^2-x^2}} & = \int\frac{a\cos(\theta)\,\mathrm d\theta}{\sqrt{a^2-a^2\sin^2(\theta)}} \\ &= \int\frac{a\cos(\theta)\,\mathrm d\theta}{\sqrt{a^2(1-\sin^2(\theta))}} \\ &= \int\frac{a\cos(\theta)\,\mathrm d\theta}{\sqrt{a^2\cos^2(\theta)}} \\ &= \int \mathrm d\theta \\ &= \theta+C \\ &= \arcsin \left(\tfrac{x}{a}\right)+C \end{align}

Note that the above step requires that a > 0 and cos(θ) > 0; we can choose the a to be the positive square root of a2; and we impose the restriction on θ to be −π/2 < θ < π/2 by using the arcsin function.

For a definite integral, one must figure out how the bounds of integration change. For example, as x goes from 0 to a/2, then sin(θ) goes from 0 to 1/2, so θ goes from 0 to π/6. Then we have

\int_0^{\frac{a}{2}}\frac{\mathrm dx}{\sqrt{a^2-x^2}}=\int_0^{\frac{\pi}{6}} \mathrm d\theta = \tfrac{\pi}{6}.

Some care is needed when picking the bounds. The integration above requires that −π/2 < θ < π/2, so θ going from 0 to π/6 is the only choice. If we had missed this restriction, we might have picked θ to go from π to 5π/6, which would give us the negative of the result.

Integrals containing a2 + x2

In the integral

\int\frac{\mathrm dx}{{a^2+x^2}}

we may write

x=a\tan(\theta),\quad \mathrm dx=a\sec^2(\theta)\,\mathrm d\theta, \quad \theta=\arctan\left(\tfrac{x}{a}\right)

so that the integral becomes

\begin{align} \int\frac{\mathrm dx}{{a^2+x^2}} &= \int\frac{a\sec^2(\theta)\,\mathrm d\theta}{{a^2+a^2\tan^2(\theta)}} \\ &= \int\frac{a\sec^2(\theta)\,\mathrm d\theta}{{a^2(1+\tan^2(\theta))}} \\ &= \int \frac{a\sec^2(\theta)\,\mathrm d\theta}{{a^2\sec^2(\theta)}} \\ &= \int \frac{\mathrm d\theta}{a} \\ &= \tfrac{\theta}{a}+C \\ &= \tfrac{1}{a} \arctan \left(\tfrac{x}{a}\right)+C \end{align}

(provided a ≠ 0).

Integrals containing x2 − a2

Integrals like

\int\frac{\mathrm dx}{x^2 - a^2}

should be done by partial fractions rather than trigonometric substitutions. However, the integral

\int\sqrt{x^2 - a^2}\,\mathrm dx

can be done by substitution:

x = a \sec(\theta),\quad \mathrm dx = a \sec(\theta)\tan(\theta)\,\mathrm d\theta, \quad \theta = \arcsec\left(\tfrac{x}{a}\right)
\begin{align} \int\sqrt{x^2 - a^2}\,\mathrm dx &= \int\sqrt{a^2 \sec^2(\theta) - a^2} \cdot a \sec(\theta)\tan(\theta)\,\mathrm d\theta \\ &= \int\sqrt{a^2 (\sec^2(\theta) - 1)} \cdot a \sec(\theta)\tan(\theta)\,\mathrm d\theta \\ &= \int\sqrt{a^2 \tan^2(\theta)} \cdot a \sec(\theta)\tan(\theta)\,\mathrm d\theta \\ &= \int a^2 \sec(\theta)\tan^2(\theta)\,\mathrm d\theta \\ &= a^2 \int \sec(\theta)(\sec^2(\theta) - 1)\,\mathrm d\theta \\ &= a^2 \int (\sec^3(\theta) - \sec(\theta))\,\mathrm d\theta. \end{align}

We can then solve this using the formula for the integral of secant cubed.

Substitutions that eliminate trigonometric functions

Substitution can be used to remove trigonometric functions. In particular, see Tangent half-angle substitution.

For instance,

\begin{align} \int f(\sin(x), \cos(x))\,\mathrm dx &=\int\frac1{\pm\sqrt{1-u^2}} f\left(u,\pm\sqrt{1-u^2}\right)\,\mathrm du && u=\sin (x) \\ \int f(\sin(x), \cos(x))\,\mathrm dx &=\int\frac{1}{\mp\sqrt{1-u^2}} f\left(\pm\sqrt{1-u^2},u\right)\,\mathrm du && u=\cos (x) \\ \int f(\sin(x), \cos(x))\,\mathrm dx &=\int\frac2{1+u^2} f \left(\frac{2u}{1+u^2},\frac{1-u^2}{1+u^2}\right)\,\mathrm du && u=\tan\left (\tfrac{x}{2} \right ) \\ \int\frac{\cos x}{(1+\cos x)^3}\,\mathrm dx &= \int\frac2{1+u^2}\frac{\frac{1-u^2}{1+u^2}}{\left(1+\frac{1-u^2}{1+u^2}\right)^3}\,\mathrm du = \int \frac{1-u^2}{1+u^2}\,\mathrm du \end{align}

Hyperbolic substitution

Substitutions of hyperbolic functions can also be used to simplify integrals.[3]

In the integral \int \frac{1}{\sqrt{a^2+x^2}}\,\mathrm dx, make the substitution x=a\sinh{u}, \mathrm dx=a\cosh{u}\,\mathrm du.

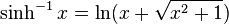Then, using the identities \cosh^2 (x) - \sinh^2 (x) = 1 and \sinh^{-1}{x} = \ln(x + \sqrt{x^2 + 1}),

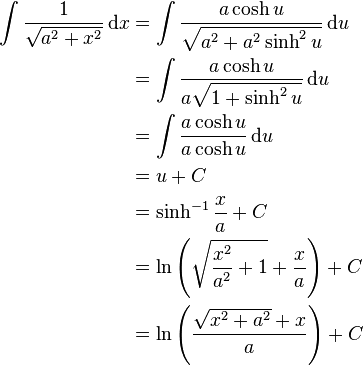
\begin{align} \int \frac{1}{\sqrt{a^2+x^2}}\,\mathrm dx &= \int \frac{a\cosh{u}}{\sqrt{a^2+a^2\sinh^2{u}}}\,\mathrm du\\ &=\int \frac{a\cosh{u}}{a\sqrt{1+\sinh^2{u}}}\,\mathrm du\\ &=\int \frac{a\cosh{u}}{a\cosh{u}}\,\mathrm du\\ &=u+C\\ &=\sinh^{-1}{\frac{x}{a}}+C\\ &=\ln\left(\sqrt{\frac{x^2}{a^2} + 1} + \frac{x}{a}\right) + C\\ &=\ln\left(\frac{\sqrt{x^2+a^2} + x}{a}\right) + C \end{align}

See also

References

  1. ↑ Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN 0-495-01166-5.
  2. ↑ Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus: Early Transcendentals (12th ed.). Addison-Wesley. ISBN 0-321-58876-2.
  3. ↑ Boyadzhiev, Khristo N. "Hyperbolic Substitutions for Integrals" (PDF). Retrieved 4 March 2013.