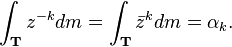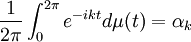Trigonometric moment problem
In mathematics, the trigonometric moment problem is formulated as follows: given a finite sequence {α0, ... αn }, does there exist a positive Borel measure μ on the interval [0, 2π] such that
In other words, an affirmative answer to the problems means that {α0, ... αn } are the first n + 1 Fourier coefficients of some positive Borel measure μ on [0, 2π].
Characterization
The trigonometric moment problem is solvable, that is, {αk} is a sequence of Fourier coefficients, if and only if the (n + 1) × (n + 1) Toeplitz matrix
The "only if" part of the claims can be verified by a direct calculation.
We sketch an argument for the converse. The positive semidefinite matrix A defines a sesquilinear product on Cn + 1, resulting in a Hilbert space
of dimensional at most n + 1, a typical element of which is an equivalence class denoted by [f]. The Toeplitz structure of A means that a "truncated" shift is a partial isometry on  . More specifically, let { e0, ...en } be the standard basis of Cn + 1. Let
. More specifically, let { e0, ...en } be the standard basis of Cn + 1. Let 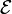 be the subspace generated by { [e0], ... [en - 1] } and
be the subspace generated by { [e0], ... [en - 1] } and  be the subspace generated by { [e1], ... [en] }. Define an operator
be the subspace generated by { [e1], ... [en] }. Define an operator
by
Since
V can be extended to a partial isometry acting on all of  . Take a minimal unitary extension U of V, on a possibly larger space (this always exists). According to the spectral theorem, there exists a Borel measure m on the unit circle T such that for all integer k
. Take a minimal unitary extension U of V, on a possibly larger space (this always exists). According to the spectral theorem, there exists a Borel measure m on the unit circle T such that for all integer k
For k = 0,...,n, the left hand side is
So
Finally, parametrize the unit circle T by eit on [0, 2π] gives
for some suitable measure μ.
Parametrization of solutions
The above discussion shows that the trigonometric moment problem has infinitely many solutions if the Toeplitz matrix A is invertible. In that case, the solutions to the problem are in bijective correspondence with minimal unitary extensions of the partial isometry V.
References
- N.I. Akhiezer, The Classical Moment Problem, Olivier and Boyd, 1965.
- N.I. Akhiezer, M.G. Krein, Some Questions in the Theory of Moments, Amer. Math. Soc., 1962.
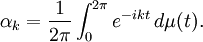
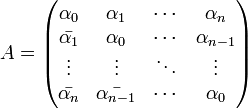
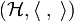
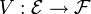
![V[e_k] = [e_{k+1}] \quad \mbox{for} \quad k = 0 \ldots n-1.](../I/m/e1418b41587da394972200f1fd589338.png)
![\langle V[e_j], V[e_k] \rangle = \langle [e_{j+1}], [e_{k+1}] \rangle = A_{j+1, k+1} = A_{j, k} = \langle [e_{j+1}], [e_{k+1}] \rangle,](../I/m/8ff287615a3e09843027727740b0f03d.png)
![\langle (U^*)^k [ e_ {n+1} ], [ e_ {n+1} ] \rangle = \int_{\mathbf{T}} z^{k} dm .](../I/m/5f133a000c71615e53a147b4ba2bd195.png)
![\langle (U^*)^k [ e_ {n+1} ], [ e_ {n+1} ] \rangle
= \langle (V^*)^k [ e_ {n+1} ], [ e_{n+1} ] \rangle
= \langle [e_{n+1-k}], [ e_{n+1} ] \rangle
= A_{n+1, n+1-k}
= \bar{\alpha_k}.](../I/m/db2c1a573bbf1b1976915e541ebc49b4.png)