Trifid cipher
In classical cryptography, the trifid cipher is a cipher invented around 1901 by Felix Delastelle, which extends the concept of the bifid cipher to a third dimension, allowing each symbol to be fractionated into 3 elements instead of two.
While the bifid uses the Polybius square to turn each symbol into coordinates on a 5 × 5 (or 6 × 6) square, the trifid turns them into coordinates on a 3 × 3 × 3 cube.
As with the bifid, this is then combined with transposition to achieve diffusion.
However a higher degree of diffusion is achieved because each output symbol depends on 3 input symbols instead of two.
Thus the trifid was the first practical trigraphic substitution.
Operation
Several variants probably exist of the Trifid cipher, and there are known Cyrillic variations of it as well.
Below is one example but most decoders work slightly differently.
All Triffid systems use TABLE,ROW,COLUMN or some variation of it.
The principle remains the same but the result will be completely different.
The Dutch version of this page has another example. And there are also different ways to fill out a keyword in the tables: spread out horizontally or fill up one table first.
First, a mixed alphabet cubic analogue of the Polybius square is drawn up:
| Layer 1 | Layer 2 | Layer 3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||||
| 1 | F | J | O | 1 | V | Z | L | 1 | E | U | Q | ||
| 2 | R | X | C | 2 | G | D | P | 2 | N | H | A | ||
| 3 | Y | B | S | 3 | M | W | T | 3 | . | K | I | ||
In theory, the message is then converted to its coordinates in this grid; in practice, it is more convenient to write the triplets of trits out in a table, like so:
| F 111 | C 132 | W 223 | U 321 |
| R 112 | S 133 | L 231 | H 322 |
| Y 113 | V 211 | P 232 | K 323 |
| J 121 | G 212 | T 233 | Q 331 |
| X 122 | M 213 | E 311 | A 332 |
| B 123 | Z 221 | N 312 | I 333 |
| O 131 | D 222 | . 313 |
Then the coordinates are written out vertically beneath the message:
T R E A T Y E N D S B O E R W A R . 2 1 3 3 2 1 3 3 2 1 1 1 3 1 2 3 1 3 3 1 1 3 3 1 1 1 2 3 2 3 1 1 2 3 1 1 3 2 1 2 3 3 1 2 2 3 3 1 1 2 3 2 2 3
They are then read out in rows:
2 1 3 3 2 1 3 3 2 1 1 1 3 1 2 3 1 3 3 1 1 3 3 1 1 1 2 3 2 3 1 1 2 3 1 1 3 2 1 2 3 3 1 2 2 3 3 1 1 2 3 2 2 3
Then divided up into triplets again, and the triplets turned back into letters using the table:
213 321 332 111 312 313 311 331 112 323 112 311 321 233 122 331 123 223 M U A F N . E Q R K R E U T X Q B W
In this way, each ciphertext character depends on three plaintext characters, so the trifid is a trigraphic cipher. To decrypt, the procedure is simply reversed.
Dimensions
As the bifid concept is extended to higher dimensions, we are much less free in our choice of parameters.
Since 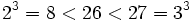 , our cube needs to have a side length of at least three in order to fit in the 26 letters of the alphabet. But if we go even to 4, then our symbol set would have
, our cube needs to have a side length of at least three in order to fit in the 26 letters of the alphabet. But if we go even to 4, then our symbol set would have 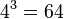 symbols, which is probably too much for classical cryptography. Thus, the trifid is only ever implemented with a 3 × 3 × 3 cube, and each coordinate is indicated by a trinary digit, or trit. Incidentally, note that since this gives us 27 symbols, we will have one extra. In the example above, the period or full-stop was used.
symbols, which is probably too much for classical cryptography. Thus, the trifid is only ever implemented with a 3 × 3 × 3 cube, and each coordinate is indicated by a trinary digit, or trit. Incidentally, note that since this gives us 27 symbols, we will have one extra. In the example above, the period or full-stop was used.
If we increase the dimensions further to four, noting that 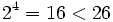 , we still need a side length of 3 - giving a symbol set of size
, we still need a side length of 3 - giving a symbol set of size 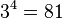 , far more than we need. If we go one step further, to five dimensions, then we only need a side length of 2, since
, far more than we need. If we go one step further, to five dimensions, then we only need a side length of 2, since 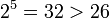 . But such a binary encoding - 5 bits - is what occurs in Baudot code for telegraphic purposes. Breaking letters into bits and manipulating the bits individually is the hallmark of modern cryptography. Thus, in a sense, the trifid cipher can be thought to stand on the border between classical cryptography's ancient Polybius square, and the binary manipulations of the modern world.
. But such a binary encoding - 5 bits - is what occurs in Baudot code for telegraphic purposes. Breaking letters into bits and manipulating the bits individually is the hallmark of modern cryptography. Thus, in a sense, the trifid cipher can be thought to stand on the border between classical cryptography's ancient Polybius square, and the binary manipulations of the modern world.
See also
Other ciphers by Delastelle:
- Four-square cipher (related to Playfair)
- Bifid cipher (similar to trifid)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||