Trianglepoint

Trianglepoint is a form of embroidery in which a series of equilateral triangles are stitched in different colors to create geometric designs, three-dimensional designs or pictures. The term was coined by needlepoint designer Sherlee Lantz (or more accurately suggested by a friend) for her 1976 book Trianglepoint (New York: Viking).
Basic Stitch
Sherlee Lantz created a system to create an equilateral triangle in needlepoint then put them together to create original designs.
It starts with a vertical stitch over two threads, then an adjacent vertical stitch over four threads, then a vertical stitch over six threads, then a vertical stitch over eight threads at the apex (highest point) After the apex, you place a stitch over six threads, then a stitch over four threads, then a final stitch over two threads. That is, for every stitch placed to the left or right, you increase or decrease the number of threads you stitch over by two.

Depending on how tall you make the apex (e.g. 6 threads, 10 threads, 12 threads, etc.) you can create triangles of different sizes.
Combining Triangles, Hexagons, Diamonds and Parallelograms
Although the design of the triangle is simple to execute, the power of this technique is the ability to combine triangles together to create patterns and other shapes including hexagons, diamonds and parallelograms. Note that shapes made of combined equilateral triangles are also called polyiamonds.
Note that where two short points of a triangle come together, Lantz uses an extra long stitch to join them two shapes.
These shapes along with the triangles can be combined to form a wide variety of geometric designs and tessellations or tilings.
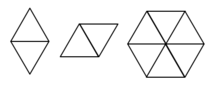
Development of Trianglepoint
Sherlee Lantz calls this a triangle stitch, but it simply a variation of basic satin stitch in canvas work. That is you create stitch patterns by covering different numbers of threads on the canvas with your fiber in different configurations.
Here is Sherlee Lantz’s explanation of how she was inspired to work with triangles (Lantz 1976: pg 9).
- My eyes wandered … unbidden to the hexagons clambering [over an antique Turkish pattern] like so many enfants terribles. They were playing there. Upsetting me. I had long wanted to corral them (and other patterns in the same geometric network) to the squares of the needlepoint canvas. But the hexagon, with the six triangles that compose it, is based on the 60° angles, the threads of the canvas of on the 90° angle and, no matter how I called the tune, I could not get them to dance together.
- It was snowing. Outside my window a corps of hexagon crystals flocked the pewter dusk. Some might call their conspiracy beautiful. I called it a conspiracy and retreated to another room to find distraction in putting up my recently completed playing card hanging [adapted from a late 15th-century French source and featuring a black and white triangular floor pattern]. My eyes focused on the medieval triangular background I had selected for the King of Knaves. I had been puzzled by its magnetism, [but] suddenly why it had held me in thrall. Those triangles were making hexagons. And if they could make one hexagonal patterns, surely they might make others.
Historical Sources
Lantz refers to Islamic and European sources as inspirations for trianglepoint designs, but tessellations based on triangles and regular hexagons can be found in a wide number of cultures Roman, Chinese and Byzantine cultures.
- Islamic Geometric Art (Dartmouth Geometry in Art)
- English Example (Tiling Plain & Fancy)
- Chinese Example (Tiling Plain & Fancy)
- Byzantine Example (Tiling Plain & Fancy)
- Roman Example (Tiling Plain & Fancy)
However, some might argue that the most recognized examples are associated with Islamic cultures.
Three Dimensional Illusions with Triangle Point
If you use a light, medium and dark value of fiber, you can easily create three dimensional effects with triangle point. A simple example is a cube illusion created by a six-triangle hexagon filled in with light values in two triangles, then a medium value in two areas, then two areas of darks. These cubes can be clustered together to form more intricate three-dimensional patterns. Below are some examples of three-dimensional effects created with triangles and diamonds.
Design How To
Isometric graph paper
To create trianglepoint designs, Lantz suggests using triangular isometric graph paper, then coloring in the shapes to create different designs.
Sizing Triangles
In “classic” triangle point as envisioned by Lantz, you stitch one size of triangle for each triangle on your isometric graph paper. In Lantz’s book the apex of each trianglular unit is usually 6, 8 or 10 stitches tall.
However, it is possible to combine triangles of different sizes in one pattern. For instance a large triangle of one color can replace a set of smaller ones. As long as each triangle is formed by stitches increasing or decreasing heights in increments of two, the patterns are usually workable.
Further reading
- Lantz, Sherlee (1976) Trianglepoint. Viking Press.
- Bourgoin, J. (1973) Arabic Geometrical Pattern and Design (Dover Pictorial Archive Series). Dover Publications
- Locke, John (1981) Isometric Perspective Designs and How to Create Them. Dover Publications
- Turner, Harry (1978) Triad Optical Illustions. Dover Publications
| ||||||||||||||||||||||||||||||||||||


