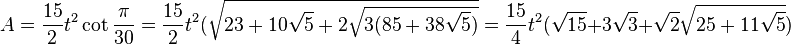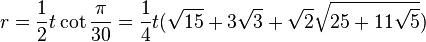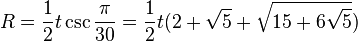Triacontagon

Regular triacontagon

A regular triacontagon
Type Regular polygon
Edges and vertices 30
Schläfli symbol {30}
t{15}
Coxeter diagram
Symmetry group Dihedral (D30), order 2×30
Internal angle (degrees) 168°
Dual polygon self
Properties convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a triacontagon is a thirty-sided polygon. The sum of any triacontagon's interior angles is 5040 degrees.

The regular triacontagon is a constructible polygon, by an edge-bisection of a regular pentadecagon, and can also be constructed as a truncated pentadecagon, t{15}.

Regular triacontagon properties

One interior angle in a regular triacontagon is 168°, meaning that one exterior angle would be 12°. The triacontagon is the largest regular polygon whose interior angle is the sum of the interior angles of smaller polygons: 168° is the sum of the interior angles of the equilateral triangle (60°) and the regular pentagon (108°).

The area of a regular triacontagon is (with t = edge length)

A = \frac{15}{2} t^2 \cot \frac{\pi}{30} = \frac{15}{2} t^2 (\sqrt{23 + 10 \sqrt{5} + 2 \sqrt{3(85 + 38 \sqrt{5})}} = \frac{15}{4} t^2 (\sqrt{15} + 3\sqrt{3} + \sqrt{2}\sqrt{25+11\sqrt{5}})

The inradius of a regular triacontagon is

r = \frac{1}{2} t \cot \frac{\pi}{30} = \frac{1}{4} t(\sqrt{15} + 3\sqrt{3} + \sqrt{2}\sqrt{25+11\sqrt{5}})

The circumradius of a regular triacontagon is

R = \frac{1}{2} t \csc \frac{\pi}{30} = \frac{1}{2} t(2 + \sqrt{5} + \sqrt{15+6\sqrt{5}})

Construction

A regular triacontagon is constructible using a compass and straightedge.[1]

Triacontagram

A triacontagram is a 30-sided star polygon. There are 3 regular forms given by Schläfli symbols {30/7}, {30/11}, and {30/13}, and 11 compound star figures with the same vertex configuration.

Form Compounds Star polygon Compound
Picture
{30/2}=2{15}
{30/3}=3{10}
{30/4}=2{15/2}
{30/5}=5{6}
{30/6}=6{5}
{30/7}
{30/8}=2{15/4}
Interior angle 156° 144° 132° 120° 108° 96° 84°
Form Compounds Star polygon Compound Star polygon Compounds
Picture
{30/9}=3{10/3}
{30/10}=10{3}
{30/11}
{30/12}=6{5/2}
{30/13}
{30/14}=2{15/7}
{30/15}=15{2}
Interior angle 72° 60° 48° 36° 24° 12° 0°

There are also isogonal triacontagrams constructed as deeper truncations of the regular pentadecagon {15} and pentadecagram {15/7}, and inverted pentadecagrams {15/11}, and {15/13}. Other truncations form double coverings: t{15/14}={30/14}=2{15/7}, t{15/8}={30/8}=2{15/4}, t{15/4}={30/4}=2{15/4}, and t{15/2}={30/2}=2{15}.[2]

Quasiregular Isogonal Quasiregular
Double coverings

t{15} = {30}
t{15/14}=2{15/7}

t{15/7}={30/7}
t{15/8}=2{15/4}

t{15/11}={30/11}
t{15/4}=2{15/2}

t{15/13}={30/13}
t{15/2}=2{15}

Petrie polygons

The regular triacontagon is the Petrie polygon for three 8-dimensional polytopes with E8 symmetry, shown in orthogonal projections in the E8 Coxeter plane. It is also the Petrie polygon for two 4-dimensional polytopes, shown in the H4 Coxeter plane.

E8 H4

421
241
142
120-cell
600-cell

The regular triacontagram {30/7} is also the Petrie polygon for the great grand stellated 120-cell and grand 600-cell.

References

  1. ↑ Constructible Polygon
  2. ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum