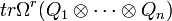Transvectant

In mathematical invariant theory, a transvectant is an invariant formed from n invariants in n variables using Cayley's Ω process.

Definition

If Q₁,...,Q_n are functions of n variables x = (x₁,...,x_n) and r ≥ 0 is an integer then the r^th transvectant of these functions is a function of n variables given by

tr \Omega^r(Q_1\otimes\cdots \otimes Q_n)

where Ω is Cayley's Ω process, the tensor product means take a product of functions with different variables x¹,..., xⁿ, and tr means set all the vectors x^k equal.

Examples

The zeroth transvectant is the product of the n functions.

The first transvectant is the Jacobian determinant of the n functions.

The second transvectant is a constant times the completely polarized form of the Hessian of the n functions.

References

Olver, Peter J. (1999), Classical invariant theory, Cambridge University Press, ISBN 978-0-521-55821-1
Olver, Peter J.; Sanders, Jan A. (2000), "Transvectants, modular forms, and the Heisenberg algebra", Advances in Applied Mathematics 25 (3): 252–283, doi:10.1006/aama.2000.0700, ISSN 0196-8858, MR 1783553