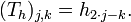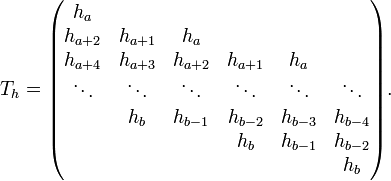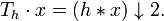Transfer matrix

This article is about the transfer matrix in wavelet theory. For the transfer matrix method in statistical physics, see Transfer-matrix method. For the transfer matrix method in optics, see Transfer-matrix method (optics).

In applied mathematics, the transfer matrix is a formulation in terms of a block-Toeplitz matrix of the two-scale equation, which characterizes refinable functions. Refinable functions play an important role in wavelet theory and finite element theory.

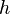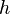For the mask $h$ , which is a vector with component indexes from $a$ to $b$ , the transfer matrix of $h$ , we call it 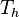$T_h$ here, is defined as

(T_h)_{j,k} = h_{2\cdot j-k}.

More verbosely

T_h = \begin{pmatrix} h_{a } & & & & & \\ h_{a+2} & h_{a+1} & h_{a } & & & \\ h_{a+4} & h_{a+3} & h_{a+2} & h_{a+1} & h_{a } & \\ \ddots & \ddots & \ddots & \ddots & \ddots & \ddots \\ & h_{b } & h_{b-1} & h_{b-2} & h_{b-3} & h_{b-4} \\ & & & h_{b } & h_{b-1} & h_{b-2} \\ & & & & & h_{b } \end{pmatrix}.

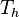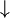The effect of $T_h$ can be expressed in terms of the downsampling operator " $\downarrow$ ":

T_h\cdot x = (h*x)\downarrow 2.

Properties

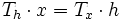$T_h\cdot x = T_x\cdot h$ .
If you drop the first and the last column and move the odd-indexed columns to the left and the even-indexed columns to the right, then you obtain a transposed Sylvester matrix.
The determinant of a transfer matrix is essentially a resultant.

More precisely:

Let

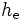h_{\mathrm{e}}

be the even-indexed coefficients of

h

(

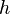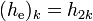(h_{\mathrm{e}})_k = h_{2k}

) and let

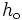h_{\mathrm{o}}

be the odd-indexed coefficients of

h

(

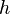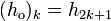(h_{\mathrm{o}})_k = h_{2k+1}

Then

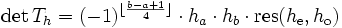\det T_h = (-1)^{\lfloor\frac{b-a+1}{4}\rfloor}\cdot h_a\cdot h_b\cdot\mathrm{res}(h_{\mathrm{e}},h_{\mathrm{o}})

, where

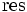\mathrm{res}

is the resultant.

This connection allows for fast computation using the Euclidean algorithm.

For the trace of the transfer matrix of convolved masks holds

\mathrm{tr}~T_{g*h} = \mathrm{tr}~T_g \cdot \mathrm{tr}~T_h

For the determinant of the transfer matrix of convolved mask holds

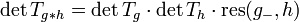
\det T_{g*h} = \det T_g \cdot \det T_h \cdot \mathrm{res}(g_-,h)

where

g_-

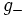denotes the mask with alternating signs, i.e.

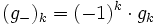(g_-)_k = (-1)^k \cdot g_k

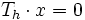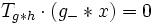If $T_{h}\cdot x = 0$ , then $T_{g*h}\cdot (g_-*x) = 0$ .

This is a concretion of the determinant property above. From the determinant property one knows that

T_{g*h}

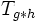is singular whenever

T_{h}

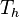is singular. This property also tells, how vectors from the null space of

T_{h}

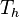can be converted to null space vectors of

T_{g*h}

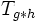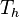If $x$ is an eigenvector of $T_{h}$ with respect to the eigenvalue $\lambda$ , i.e.

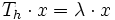T_{h}\cdot x = \lambda\cdot x

then

x*(1,-1)

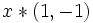is an eigenvector of

T_{h*(1,1)}

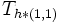with respect to the same eigenvalue, i.e.

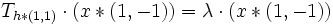T_{h*(1,1)}\cdot (x*(1,-1)) = \lambda\cdot (x*(1,-1))

Let 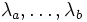$\lambda_a,\dots,\lambda_b$ be the eigenvalues of 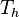$T_h$ , which implies 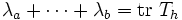$\lambda_a+\dots+\lambda_b = \mathrm{tr}~T_h$ and more generally 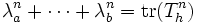$\lambda_a^n+\dots+\lambda_b^n = \mathrm{tr}(T_h^n)$ . This sum is useful for estimating the spectral radius of 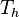$T_h$ . There is an alternative possibility for computing the sum of eigenvalue powers, which is faster for small $n$ .

Let

C_k h

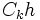be the periodization of

h

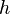with respect to period

2^k-1

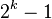. That is

C_k h

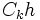is a circular filter, which means that the component indexes are residue classes with respect to the modulus

2^k-1

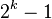. Then with the upsampling operator

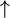\uparrow

it holds

\mathrm{tr}(T_h^n) = \left(C_k h * (C_k h\uparrow 2) * (C_k h\uparrow 2^2) * \cdots * (C_k h\uparrow 2^{n-1})\right)_{[0]_{2^n-1}}

Actually not

n-2

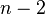convolutions are necessary, but only

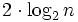2\cdot \log_2 n

ones, when applying the strategy of efficient computation of powers. Even more the approach can be further sped up using the Fast Fourier transform.

From the previous statement we can derive an estimate of the spectral radius of 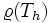$\varrho(T_h)$ . It holds

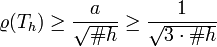
\varrho(T_h) \ge \frac{a}{\sqrt{\# h}} \ge \frac{1}{\sqrt{3\cdot \# h}}

where

\# h

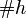is the size of the filter and if all eigenvalues are real, it is also true that

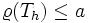\varrho(T_h) \le a

where

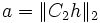a = \Vert C_2 h \Vert_2

References

Strang, Gilbert (1996). "Eigenvalues of 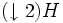$(\downarrow 2){H}$ and convergence of the cascade algorithm". IEEE Transactions on Signal Processing 44. pp. 233–238.
Thielemann, Henning (2006). Optimally matched wavelets (PhD thesis). (contains proofs of the above properties)

Transfer matrix

Properties

See also

References