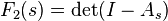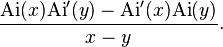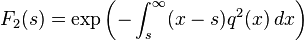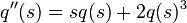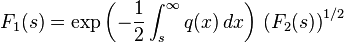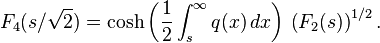Tracy–Widom distribution

The Tracy–Widom distribution, introduced by Craig Tracy and Harold Widom (1993, 1994), is the probability distribution of the normalized largest eigenvalue of a random Hermitian matrix.[1]
In practical terms, Tracy-Widom is the crossover function between the two phases of weakly versus strongly coupled components in a system.[2]
It also appears in the distribution of the length of the longest increasing subsequence of random permutations (Baik, Deift & Johansson 1999), in current fluctuations of the asymmetric simple exclusion process (ASEP) with step initial condition (Johansson 2000, Tracy & Widom 2009), and in simplified mathematical models of the behavior of the longest common subsequence problem on random inputs (Majumdar & Nechaev 2005). See (Takeuchi & Sano 2010, Takeuchi et al. 2011) for experimental testing (and verifying) that the interface fluctuations of a growing droplet (or substrate) are described by the TW distribution 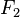 (or
(or 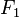 ) as predicted by (Prähofer & Spohn 2000).
) as predicted by (Prähofer & Spohn 2000).
The distribution F1 is of particular interest in multivariate statistics (Johnstone 2007, 2008, 2009). For a discussion of the universality of Fβ, β = 1, 2, and 4, see Deift (2007). For an application of F1 to inferring population structure from genetic data see Patterson, Price & Reich (2006).
Definition
The Tracy-Widom distribution is defined as the limit:[3]
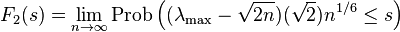 ,
,
The shift by  is used to keep the distributions centered at 0. The multiplication by
is used to keep the distributions centered at 0. The multiplication by  is used because the standard deviation of the distributions scales as
is used because the standard deviation of the distributions scales as  .
.
Equivalent formulations
The cumulative distribution function of the Tracy–Widom distribution can be given as the Fredholm determinant
of the operator As on square integrable functions on the half line (s, ∞) with kernel given in terms of Airy functions Ai by
It can also be given as an integral
in terms of a solution of a Painlevé equation of type II
where q, called the Hastings–McLeod solution, satisfies the boundary condition
Other Tracy-Widom Distributions
The distribution F2 is associated to unitary ensembles in random matrix theory. There are analogous Tracy–Widom distributions F1 and F4 for orthogonal (β = 1) and symplectic ensembles (β = 4) that are also expressible in terms of the same Painlevé transcendent q (Tracy & Widom 1996):
and
For an extension of the definition of the Tracy–Widom distributions Fβ to all β > 0 see Ramírez, Rider & Virág (2006).
Numerical approximations
Numerical techniques for obtaining numerical solutions to the Painlevé equations of the types II and V, and numerically evaluating eigenvalue distributions of random matrices in the beta-ensembles were first presented by Edelman & Persson (2005) using MATLAB. These approximation techniques were further analytically justified in Bejan (2005) and used to provide numerical evaluation of Painlevé II and Tracy–Widom distributions (for β=1,2, and 4) in S-PLUS. These distributions have been tabulated in Bejan (2005) to four significant digits for values of the argument in increments of 0.01; a statistical table for p-values was also given in this work. Bornemann (2009) gave accurate and fast algorithms for the numerical evaluation of Fβ and the density functions fβ(s) = dFβ/ds for β = 1, 2, and 4. These algorithms can be used to compute numerically the mean, variance, skewness and kurtosis of the distributions Fβ.
| β | Mean | Variance | Skewness | Kurtosis |
|---|---|---|---|---|
| 1 | −1.2065335745820 | 1.607781034581 | 0.29346452408 | 0.1652429384 |
| 2 | −1.771086807411 | 0.8131947928329 | 0.224084203610 | 0.0934480876 |
| 4 | −2.306884893241 | 0.5177237207726 | 0.16550949435 | 0.0491951565 |
Functions for working with the Tracy–Widom laws are also presented in the R package 'RMTstat' by Johnstone et al. (2009) and MATLAB package 'RMLab' by Dieng (2006).
For a simple approximation based on a shifted gamma distribution see Chiani (2012).
Footnotes
- ↑ Dominici, D. (2008) Special Functions and Orthogonal Polynomials American Math. Soc.
- ↑ Mysterious Statistical Law May Finally Have an Explanation, wired.com 2014-10-27
- ↑ Tracy, C. A.; Widom, H. (1996), "On orthogonal and symplectic matrix ensembles", Communications in Mathematical Physics 177 (3): 727–754, Bibcode:1996CMaPh.177..727T, doi:10.1007/BF02099545, MR 1385083
References
- Baik, J.; Deift, P.; Johansson, K. (1999), "On the distribution of the length of the longest increasing subsequence of random permutations", Journal of the American Mathematical Society 12 (4): 1119–1178, doi:10.1090/S0894-0347-99-00307-0, JSTOR 2646100, MR 1682248.
- Deift, P. (2007), "Universality for mathematical and physical systems", International Congress of Mathematicians (Madrid, 2006), European Mathematical Society, pp. 125–152, MR 2334189.
- Johansson, K. (2000), "Shape fluctuations and random matrices", Communications in Mathematical Physics 209 (2): 437–476, arXiv:math/9903134, Bibcode:2000CMaPh.209..437J, doi:10.1007/s002200050027.
- Johansson, K. (2002), "Toeplitz determinants, random growth and determinantal processes", Proc. International Congress of Mathematicians (Beijing, 2002) 3, Beijing: Higher Ed. Press, pp. 53–62, MR 1957518.
- Johnstone, I. M. (2007), "High dimensional statistical inference and random matrices", International Congress of Mathematicians (Madrid, 2006), European Mathematical Society, pp. 307–333, MR 2334195.
- Johnstone, I. M. (2008), "Multivariate analysis and Jacobi ensembles: largest eigenvalue, Tracy–Widom limits and rates of convergence", Annals of Statistics 36 (6): 2638–2716, arXiv:0803.3408, doi:10.1214/08-AOS605, PMC 2821031, PMID 20157626.
- Johnstone, I. M. (2009), "Approximate null distribution of the largest root in multivariate analysis", Annals of Applied Statistics 3 (4): 1616–1633, arXiv:1009.5854, doi:10.1214/08-AOAS220, PMC 2880335, PMID 20526465.
- Majumdar, Satya N.; Nechaev, Sergei (2005), "Exact asymptotic results for the Bernoulli matching model of sequence alignment", Physical Review E 72 (2): 020901, 4, doi:10.1103/PhysRevE.72.020901, MR 2177365.
- Patterson, N.; Price, A. L.; Reich, D. (2006), "Population structure and eigenanalysis", PLoS Genetics 2 (12): e190, doi:10.1371/journal.pgen.0020190, PMC 1713260, PMID 17194218.
- Prähofer, M.; Spohn, H. (2000), "Universal distributions for growing processes in 1+1 dimensions and random matrices", Physical Review Letters 84 (21): 4882–4885, arXiv:cond-mat/9912264, Bibcode:2000PhRvL..84.4882P, doi:10.1103/PhysRevLett.84.4882, PMID 10990822.
- Takeuchi, K. A.; Sano, M. (2010), "Universal fluctuations of growing interfaces: Evidence in turbulent liquid crystals", Physical Review Letters 104 (23): 230601, arXiv:1001.5121, Bibcode:2010PhRvL.104w0601T, doi:10.1103/PhysRevLett.104.230601, PMID 20867221
- Takeuchi, K. A.; Sano, M.; Sasamoto, T.; Spohn, H. (2011), "Growing interfaces uncover universal fluctuations behind scale invariance", Scientific Reports 1: 34, arXiv:1108.2118, Bibcode:2011NatSR...1E..34T, doi:10.1038/srep00034
- Tracy, C. A.; Widom, H. (1993), "Level-spacing distributions and the Airy kernel", Physics Letters B 305 (1-2): 115–118, arXiv:hep-th/9210074, Bibcode:1993PhLB..305..115T, doi:10.1016/0370-2693(93)91114-3.
- Tracy, C. A.; Widom, H. (1994), "Level-spacing distributions and the Airy kernel", Communications in Mathematical Physics 159 (1): 151–174, arXiv:hep-th/9211141, Bibcode:1994CMaPh.159..151T, doi:10.1007/BF02100489, MR 1257246.
- Tracy, C. A.; Widom, H. (2002), "Distribution functions for largest eigenvalues and their applications", Proc. International Congress of Mathematicians (Beijing, 2002) 1, Beijing: Higher Ed. Press, pp. 587–596, MR 1989209.
- Tracy, C. A.; Widom, H. (2009), "Asymptotics in ASEP with step initial condition", Communications in Mathematical Physics 290 (1): 129–154, arXiv:0807.1713, Bibcode:2009CMaPh.290..129T, doi:10.1007/s00220-009-0761-0.
Additional reading
- Bejan, Andrei Iu. (2005), Largest eigenvalues and sample covariance matrices. Tracy–Widom and Painleve II: Computational aspects and realization in S-Plus with applications, M.Sc. dissertation, Department of Statistics, The University of Warwick.
- Bornemann, F. (2010), "On the numerical evaluation of distributions in random matrix theory: A review with an invitation to experimental mathematics", Markov Processes and Related Fields 16 (4): 803–866, arXiv:0904.1581, Bibcode:2009arXiv0904.1581B.
- Chiani, M. (2012), Distribution of the largest eigenvalue for real Wishart and Gaussian random matrices and a simple approximation for the Tracy–Widom distribution, arXiv:1209.3394.
- Edelman, A.; Persson, P.-O. (2005), Numerical Methods for Eigenvalue Distributions of Random Matrices, arXiv:math-ph/0501068, Bibcode:2005math.ph...1068E.
- Ramírez, J. A.; Rider, B.; Virág, B. (2006), Beta ensembles, stochastic Airy spectrum, and a diffusion, arXiv:math/0607331, Bibcode:2006math......7331R.
External links
- Kuijlaars, Universality of distribution functions in random matrix theory.
- Tracy, C. A.; Widom, H., The distributions of random matrix theory and their applications.
- Johnstone, Iain; Ma, Zongming; Perry, Patrick; Shahram, Morteza (2009), Package 'RMTstat'.
- Quanta Magazine: At the Far Ends of a New Universal Law