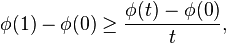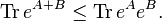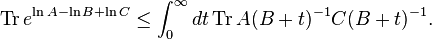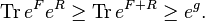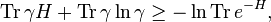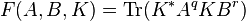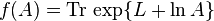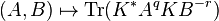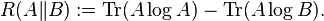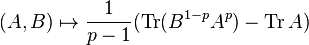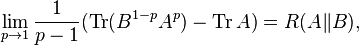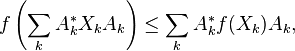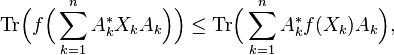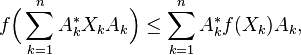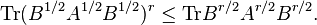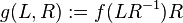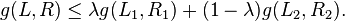Trace inequalities
In mathematics, there are many kinds of inequalities involving matrices and linear operators on Hilbert spaces. This article covers some important operator inequalities connected with traces of matrices.[1][2][3][4]
Basic definitions
Let Hn denote the space of Hermitian n×n matrices, Hn+ denote the set consisting of positive semi-definite n×n Hermitian matrices and Hn++ denote the set of positive definite Hermitian matrices. For operators on an infinite dimensional Hilbert space we require that they be trace class and self-adjoint, in which case similar definitions apply, but we discuss only matrices, for simplicity.
For any real-valued function f on an interval I ⊂ ℝ, one may define a matrix function f(A) for any operator A ∈ Hn with eigenvalues λ in I by defining it on the eigenvalues and corresponding projectors P as
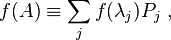 given the spectral decomposition
given the spectral decomposition 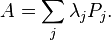
Operator monotone
A function f: I → ℝ defined on an interval I ⊂ ℝ is said to be operator monotone if ∀n, and all A,B ∈ Hn with eigenvalues in I, the following holds,
where the inequality A ≥ B means that the operator A − B ≥ 0 is positive semi-definite. One may check f(A)=A2 is, in fact, not monotone!
Operator convex
A function 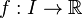 is said to be operator convex if for all
is said to be operator convex if for all  and all A,B ∈ Hn with eigenvalues in I, and
and all A,B ∈ Hn with eigenvalues in I, and 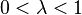 , the following holds
, the following holds
Note that the operator 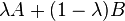 has eigenvalues in
has eigenvalues in 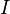 , since
, since  and
and  have eigenvalues in I.
have eigenvalues in I.
A function  is operator concave if
is operator concave if 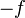 is operator convex, i.e. the inequality above for
is operator convex, i.e. the inequality above for  is reversed.
is reversed.
Joint convexity
A function 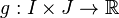 , defined on intervals
, defined on intervals 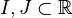 is said to be jointly convex if for all
is said to be jointly convex if for all  and all
and all
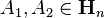 with eigenvalues in
with eigenvalues in 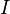 and all
and all 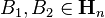 with eigenvalues in
with eigenvalues in 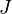 , and any
, and any 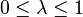 the following holds
the following holds
A function g is jointly concave if −g is jointly convex, i.e. the inequality above for g is reversed.
Trace function
Given a function f: ℝ → ℝ, the associated trace function on Hn is given by
where A has eigenvalues λ and Tr stands for a trace of the operator.
Convexity and monotonicity of the trace function
Let f: ℝ → ℝ be continuous, and let n be any integer. Then, if 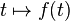 is monotone increasing, so
is
is monotone increasing, so
is 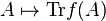 on Hn.
on Hn.
Likewise, if 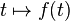 is convex, so is
is convex, so is 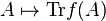 on Hn, and
it is strictly convex if f is strictly convex.
on Hn, and
it is strictly convex if f is strictly convex.
See proof and discussion in,[1] for example.
Löwner–Heinz theorem
For 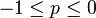 , the function
, the function 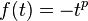 is operator monotone and operator concave.
is operator monotone and operator concave.
For 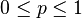 , the function
, the function 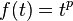 is operator monotone and operator concave.
is operator monotone and operator concave.
For 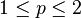 , the function
, the function 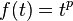 is operator convex. Furthermore,
is operator convex. Furthermore,
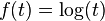 is operator concave and operator monotone, while
is operator concave and operator monotone, while 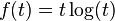 is operator convex.
is operator convex.
The original proof of this theorem is due to K. Löwner,[5] who gave a necessary and sufficient condition for f to be operator monotone. An elementary proof of the theorem is discussed in [1] and a more general version of it in.[6]
Klein's inequality
For all Hermitian n×n matrices A and B and all differentiable convex functions f: ℝ → ℝ with derivative f ' , or for all positive-definite Hermitian n×n matrices A and B, and all differentiable convex functions f:(0,∞) → ℝ, the following inequality holds,
In either case, if f is strictly convex, equality holds if and only if A = B. A popular choice in applications is f(t)=t logt, see below.
Proof
Let C = A − B so that, for 0 < t < 1,
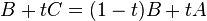 .
.
Define
By convexity and monotonicity of trace functions, φ is convex, and so for all 0 < t < 1,
and, in fact, the right hand side is monotone decreasing in t. Taking the limit t→0 yields Klein's inequality.
Note that if f is strictly convex and C≠ 0, then φ is strictly convex. The final assertion follows from this and the fact that 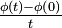 is monotone decreasing in t.
is monotone decreasing in t.
Golden–Thompson inequality
In 1965, S. Golden [7] and C.J. Thompson [8] independently discovered that
For any matrices 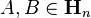 ,
,
This inequality can be generalized for three operators:[9] for non-negative operators 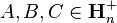 ,
,
Peierls–Bogoliubov inequality
Let 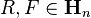 be such that Tr eR = 1.
Defining g = Tr FeR, we have
be such that Tr eR = 1.
Defining g = Tr FeR, we have
The proof of this inequality follows from the above combined with Klein's inequality. Take f(x)= exp(x), A=R+F, and B=R+g I.[10]
Gibbs variational principle
Let  be a self-adjoint operator such that
be a self-adjoint operator such that 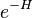 is trace class. Then for any
is trace class. Then for any 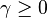 with
with 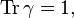
with equality if and only if 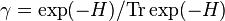 .
.
Lieb's concavity theorem
The following theorem was proved by E. H. Lieb in.[9] It proves and generalizes a conjecture of E. P. Wigner, M. M. Yanase and F. J. Dyson.[11] Six years later other proofs were given by T. Ando [12] and B. Simon,[3] and several more have been given since then.
For all 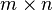 matrices
matrices  , and all
, and all  and
and  such that
such that 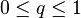 and
and 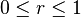 , with
, with 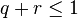 the real valued map on
the real valued map on 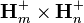 given by
given by
- is jointly concave in
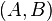
- is convex in
 .
.
Here 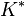 stands for the adjoint operator of
stands for the adjoint operator of 
Lieb's theorem
For a fixed Hermitian matrix 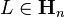 , the function
, the function
is concave on 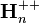 .
.
The theorem and proof are due to E. H. Lieb,[9] Thm 6, where he obtains this theorem as a corollary of Lieb's concavity Theorem. The most direct proof is due to H. Epstein;[13] see M.B. Ruskai papers,[14][15] for a review of this argument.
Ando's convexity theorem
T. Ando's proof [12] of Lieb's concavity theorem led to the following significant complement to it:
For all 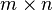 matrices
matrices  , and all
, and all 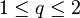 and
and 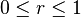 with
with 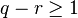 , the real valued map on
, the real valued map on 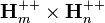 given by
given by
is convex.
Joint convexity of relative entropy
For two operators 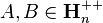 define the following map
define the following map
For density matrices  and
and  , the map
, the map 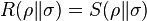 is the Umegaki's quantum relative entropy.
is the Umegaki's quantum relative entropy.
Note that the non-negativity of 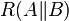 follows from Klein's inequality with
follows from Klein's inequality with 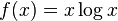 .
.
Statement
The map 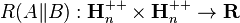 is jointly convex.
is jointly convex.
Proof
For all 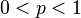 ,
, 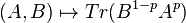 is jointly concave, by Lieb's concavity theorem, and thus
is jointly concave, by Lieb's concavity theorem, and thus
is convex. But
and convexity is preserved in the limit.
The proof is due to G. Lindblad.[16]
Jensen's operator and trace inequalities
The operator version of Jensen's inequality is due to C. Davis.[17]
A continuous, real function  on an interval
on an interval 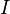 satisfies Jensen's Operator Inequality if the following holds
satisfies Jensen's Operator Inequality if the following holds
for operators 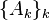 with
with 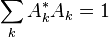 and for self-adjoint operators
and for self-adjoint operators 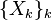 with spectrum on
with spectrum on 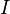 .
.
See,[17][18] for the proof of the following two theorems.
Jensen's trace inequality
Let f be a continuous function defined on an interval I and let m and n be natural numbers. If f is convex, we then have the inequality
for all (X1, ... , Xn) self-adjoint m × m matrices with spectra contained in I and all (A1, ... , An) of m × m matrices with
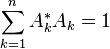 .
.
Conversely, if the above inequality is satisfied for some n and m, where n > 1, then f is convex.
Jensen's operator inequality
For a continuous function  defined on an interval
defined on an interval 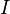 the following conditions are equivalent:
the following conditions are equivalent:
-
 is operator convex.
is operator convex. - For each natural number
 we have the inequality
we have the inequality
for all 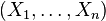 bounded, self-adjoint operators on an arbitrary Hilbert space
bounded, self-adjoint operators on an arbitrary Hilbert space  with
spectra contained in
with
spectra contained in 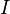 and all
and all 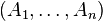 on
on  with
with 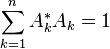 .
.
-
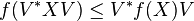 for each isometry
for each isometry  on an infinite-dimensional Hilbert space
on an infinite-dimensional Hilbert space  and
and
every self-adjoint operator  with spectrum in
with spectrum in 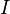 .
.
-
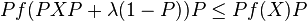 for each projection
for each projection  on an infinite-dimensional Hilbert space
on an infinite-dimensional Hilbert space  , every self-adjoint operator
, every self-adjoint operator  with spectrum in
with spectrum in 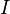 and every
and every  in
in 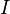 .
.
Araki-Lieb-Thirring inequality
E. H. Lieb and W. E. Thirring proved the following inequality in [19] in 1976: For any 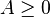 ,
, 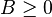 and
and 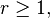
In 1990 [20] H. Araki generalized the above inequality to the following one: For any 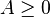 ,
, 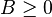 and
and 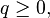
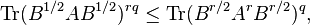 for
for 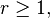
and
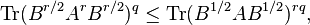 for
for 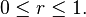
Effros's theorem
E. Effros in [21] proved the following theorem.
If 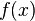 is an operator convex function, and
is an operator convex function, and  and
and  are commuting bounded linear operators, i.e. the commutator
are commuting bounded linear operators, i.e. the commutator ![[L,R]=LR-RL=0](../I/m/428cec6e73e9cfb8254856535d562f50.png) , the perspective
, the perspective
is jointly convex, i.e. if 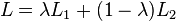 and
and 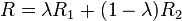 with
with ![[L_i, R_i]=0](../I/m/35db14430f8d06aba19681bf64abc013.png) (i=1,2),
(i=1,2), 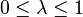 ,
,
See also
References
- ↑ 1.0 1.1 1.2 E. Carlen, Trace Inequalities and Quantum Entropy: An Introductory Course, Contemp. Math. 529 (2009).
- ↑ R. Bhatia, Matrix Analysis, Springer, (1997).
- ↑ 3.0 3.1 B. Simon, Trace Ideals and their Applications, Cambridge Univ. Press, (1979); Second edition. Amer. Math. Soc., Providence, RI, (2005).
- ↑ M. Ohya, D. Petz, Quantum Entropy and Its Use, Springer, (1993).
- ↑ K. Löwner, "Uber monotone Matrix funktionen", Math. Z. 38, 177–216, (1934).
- ↑ W.F. Donoghue, Jr., Monotone Matrix Functions and Analytic Continuation, Springer, (1974).
- ↑ S. Golden, Lower Bounds for Helmholtz Functions, Phys. Rev. 137, B 1127–1128 (1965)
- ↑ C.J. Thompson, Inequality with Applications in Statistical Mechanics, J. Math. Phys. 6, 1812–1813, (1965).
- ↑ 9.0 9.1 9.2 E. H. Lieb, Convex Trace Functions and the Wigner–Yanase–Dyson Conjecture, Advances in Math. 11, 267–288 (1973).
- ↑ D. Ruelle, Statistical Mechanics: Rigorous Results, World Scient. (1969).
- ↑ E. P. Wigner, M. M. Yanase, On the Positive Semi-Definite Nature of a Certain Matrix Expression, Can. J. Math. 16, 397–406, (1964).
- ↑ 12.0 12.1 . Ando, Convexity of Certain Maps on Positive Definite Matrices and Applications to Hadamard Products, Lin. Alg. Appl. 26, 203–241 (1979).
- ↑ H. Epstein, Remarks on Two Theorems of E. Lieb, Comm. Math. Phys., 31:317–325, (1973).
- ↑ M. B. Ruskai, Inequalities for Quantum Entropy: A Review With Conditions for Equality, J. Math. Phys., 43(9):4358–4375, (2002).
- ↑ M. B. Ruskai, Another Short and Elementary Proof of Strong Subadditivity of Quantum Entropy, Reports Math. Phys. 60, 1–12 (2007).
- ↑ G. Lindblad, Expectations and Entropy Inequalities, Commun. Math. Phys. 39, 111–119 (1974).
- ↑ 17.0 17.1 C. Davis, A Schwarz inequality for convex operator functions, Proc. Amer. Math. Soc. 8, 42–44, (1957).
- ↑ F. Hansen, G. K. Pedersen, Jensen's Operator Inequality, Bull. London Math. Soc. 35 (4): 553–564, (2003).
- ↑ E. H. Lieb, W. E. Thirring, Inequalities for the Moments of the Eigenvalues of the Schrödinger Hamiltonian and Their Relation to Sobolev Inequalities, in Studies in Mathematical Physics, edited E. Lieb, B. Simon, and A. Wightman, Princeton University Press, 269-303 (1976).
- ↑ H. Araki, On an Inequality of Lieb and Thirring, Lett. Math. Phys. 19, 167-170 (1990).
- ↑ E. Effros, A Matrix Convexity Approach to Some Celebrated Quantum Inequalities, Proc. Natl. Acad. Sci. USA, 106, n.4, 1006–1008 (2009).
- Scholarpedia primary source.
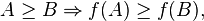
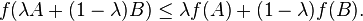
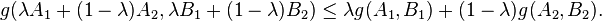
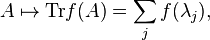
![{\rm Tr}[f(A)- f(B)- (A - B)f'(B)] \geq 0~.](../I/m/518d091ff560395d227bb7539ab2ccee.png)
![\phi(t) = {\rm Tr}[f(B + tC)]~.](../I/m/bebb30fa5a2fed288ba0b0d502d8c045.png)