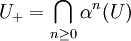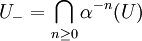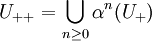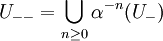Totally disconnected group
In mathematics, a totally disconnected group is a topological group that is totally disconnected. Such topological groups are necessarily Hausdorff.
Interest centres on locally compact totally disconnected groups (variously referred to as groups of td-type,[1] locally profinite groups,[2] t.d. groups[3]). The compact case has been heavily studied – these are the profinite groups – but for a long time not much was known about the general case. A theorem of van Dantzig from the 1930s, stating that every such group contains a compact open subgroup, was all that was known. Then groundbreaking work on this subject was done in 1994, when George Willis showed that every locally compact totally disconnected group contains a so-called tidy subgroup and a special function on its automorphisms, the scale function, thereby advancing the knowledge of the local structure. Advances on the global structure of totally disconnected groups have been obtained in 2011 by Caprace and Monod, with notably a clasification of characteristically simple groups and of Noetherian groups.
Locally compact case
In a locally compact, totally disconnected group, every neighbourhood of the identity contains a compact open subgroup. Conversely, if a group is such that the identity has a neighbourhood basis consisting of compact open subgroups, then it is locally compact and totally disconnected.[2]
Tidy subgroups
Let G be a locally compact, totally disconnected group, U a compact open subgroup of G and  a continuous automorphism of G.
a continuous automorphism of G.
Define:
U is said to be tidy for  if and only if
if and only if 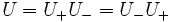 and
and 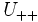 and
and 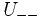 are closed.
are closed.
The scale function
The index of 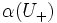 in
in 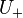 is shown to be finite and independent of the U which is tidy for
is shown to be finite and independent of the U which is tidy for  . Define the scale function
. Define the scale function 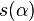 as this index. Restriction to inner automorphisms gives a function on G with interesting properties. These are in particular:
as this index. Restriction to inner automorphisms gives a function on G with interesting properties. These are in particular:
Define the function  on G by
on G by
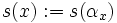 ,
where
,
where 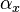 is the inner automorphism of
is the inner automorphism of  on G.
on G.
 is continuous.
is continuous.
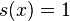 , whenever x in G is a compact element.
, whenever x in G is a compact element.
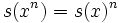 for every integer
for every integer  .
.
The modular function on G is given by 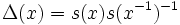 .
.
Calculations and applications
The scale function was used to prove a conjecture by Hofmann and Mukherja and has been explicitly calculated for p-adic Lie groups and linear groups over local skew fields by Helge Glöckner.
Notes
- ↑ Cartier 1979, §1.1
- ↑ 2.0 2.1 Bushnell & Henniart 2006, §1.1
- ↑ Borel & Wallach 2000, Chapter X
References
- Borel, Armand; Wallach, Nolan (2000), Continuous cohomology, discrete subgroups, and representations of reductive groups, Mathematical surveys and monographs 67 (Second ed.), Providence, Rhode Island: American Mathematical Society, ISBN 978-0-8218-0851-1, MR 1721403
- Bushnell, Colin J.; Henniart, Guy (2006), The local Langlands conjecture for GL(2), Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 335, Berlin, New York: Springer-Verlag, doi:10.1007/3-540-31511-X, ISBN 978-3-540-31486-8, MR 2234120
- Caprace, Pierre-Emmanuel; Monod, Nicolas (2011), "Decomposing locally compact groups into simple pieces", Math. Proc. Cambridge Philos. Soc. 150: 97–128, doi:10.1017/S0305004110000368, MR 2739075
- Cartier, Pierre (1979), "Representations of
 -adic groups: a survey", in Borel, Armand; Casselman, William, Automorphic Forms, Representations, and L-Functions, Proceedings of Symposia in Pure Mathematics, 33, Part 1, Providence, Rhode Island: American Mathematical Society, pp. 111–155, ISBN 978-0-8218-1435-2, MR 0546593
-adic groups: a survey", in Borel, Armand; Casselman, William, Automorphic Forms, Representations, and L-Functions, Proceedings of Symposia in Pure Mathematics, 33, Part 1, Providence, Rhode Island: American Mathematical Society, pp. 111–155, ISBN 978-0-8218-1435-2, MR 0546593 - G.A. Willis - The structure of totally disconnected, locally compact groups, Mathematische Annalen 300, 341-363 (1994)