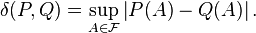Total variation distance of probability measures

In probability theory, the total variation distance is a distance measure for probability distributions. It is an example of a statistical distance metric, and is sometimes just called "the" statistical distance.

Definition

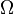The total variation distance between two probability measures P and Q on a sigma-algebra \mathcal{F} of subsets of the sample space \Omega is defined via[1]

\delta(P,Q)=\sup_{ A\in \mathcal{F}}\left|P(A)-Q(A)\right|.

Informally, this is the largest possible difference between the probabilities that the two probability distributions can assign to the same event.

Special Cases

For a finite alphabet we can relate the total variation distance to the 1-norm of the difference of the two probability distributions as follows:[2]

\delta(P,Q) = \frac 1 2 \|P-Q\|_1 = \frac 1 2 \sum_x \left| P(x) - Q(x) \right|\;.

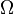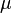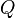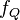Similarly, for arbitrary sample space \Omega, measure \mu, and probability measures P and Q with Radon-Nikodym derivatives f_P and f_Q with respect to 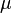\mu, an equivalent definition of the total variation distance is

\delta(P,Q) = \frac{1}{2} \|f_P-f_Q\|_{L_1(\mu)} = \frac 1 2 \int_\Omega \left| f_P - f_Q \right|d\mu\;.

Relationship with other concepts

The total variation distance is related to the Kullback–Leibler divergence by Pinsker's inequality.

See also

References

  1. ↑ Chatterjee, Sourav. "Distances between probability measures". UC Berkeley. Retrieved 21 June 2013.
  2. ↑ http://books.google.com/books?id=6Cg5Nq5sSv4C&lpg=PP1&pg=PA48#v=onepage&q&f=false