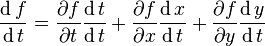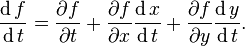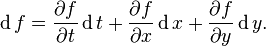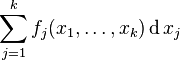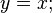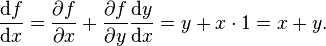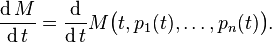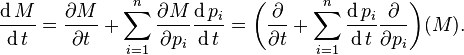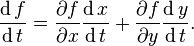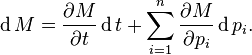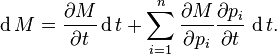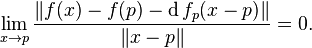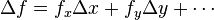Total derivative

Definitions
Derivative (generalizations) Differential infinitesimal of a function total
Concepts
Differentiation notation Second derivative Third derivative Change of variables Implicit differentiation Related rates Taylor's theorem
Rules and identities
Sum Product Chain Power Quotient Faà di Bruno's formula

Integral

Definitions
Lists of integrals
Antiderivative Integral (improper) Riemann integral Lebesgue integration Contour integration
Integration by
Parts Discs Cylindrical shells Substitution (trigonometric) Partial fractions Order Reduction formulae

Series

Convergence tests
Geometric (arithmetico-geometric) Harmonic Alternating Power Binomial Taylor
Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel

Vector

Theorems
Gradient Divergence Curl Laplacian Directional derivative Identities
Divergence Gradient Green's Stokes'

Multivariable

Formalisms
Matrix Tensor Exterior Geometric
Definitions
Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian Hessian matrix

Specialized

In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.

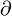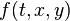The total derivative (full derivative) of a function $f$ , of several variables, e.g., $t$ , $x$ , $y$ , etc., with respect to one of its input variables, e.g., $t$ , is different from its partial derivative ( $\partial$ ). Calculation of the total derivative of $f$ with respect to $t$ does not assume that the other arguments are constant while $t$ varies; instead, it allows the other arguments to depend on $t$ . The total derivative adds in these indirect dependencies to find the overall dependency of $f$ on $t.$ ^[1]^:198-203 For example, the total derivative of $f(t,x,y)$ with respect to $t$ is
$\frac{\operatorname df}{\operatorname dt}=\frac{\partial f}{\partial t} \frac{\operatorname dt}{\operatorname dt} + \frac{\partial f}{\partial x} \frac{\operatorname dx}{\operatorname dt} + \frac{\partial f}{\partial y} \frac{\operatorname dy}{\operatorname dt}$

which simplifies to

$\frac{\operatorname df}{\operatorname dt}=\frac{\partial f}{\partial t} + \frac{\partial f}{\partial x} \frac{\operatorname dx}{\operatorname dt} + \frac{\partial f}{\partial y} \frac{\operatorname dy}{\operatorname dt}.$

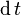Consider multiplying both sides of the equation by the differential $\operatorname dt$ :

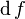${\operatorname df}=\frac{\partial f}{\partial t}\operatorname dt + \frac{\partial f}{\partial x} \operatorname dx + \frac{\partial f}{\partial y} \operatorname dy.$
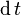The result will be the differential change $\operatorname df$ in the function $f$ . Because $f$ depends on $t$ , some of that change will be due to the partial derivative of $f$ with respect to $t$ . However, some of that change will also be due to the partial derivatives of $f$ with respect to the variables $x$ and $y$ . 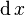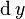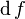So, the differential $\operatorname dt$ is applied to the total derivatives of $x$ and $y$ to find differentials $\operatorname dx$ and $\operatorname dy$ , which can then be used to find the contribution to $\operatorname df$ .
It refers to the (total) differential df of a function, either in the traditional language of infinitesimals or the modern language of differential forms.
A differential of the form
$\sum_{j=1}^k f_j(x_1,\dots, x_k) \operatorname d{x_j}$
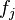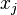(where $f_j$ refers to the partial derivative of $f$ with respect to $x_j$ ) is called a total differential or an exact differential if it is the differential of a function. Again this can be interpreted infinitesimally, or by using differential forms and the exterior derivative.
It is another name for the derivative as a linear map, i.e., if f is a differentiable function from Rⁿ to R^m, then the (total) derivative (or differential) of f at x∈Rⁿ is the linear map from Rⁿ to R^m whose matrix is the Jacobian matrix of f at x.
It is sometimes used as a synonym for the material derivative, 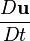$\frac{D\mathbf{u}}{Dt}$ , in fluid mechanics.

Differentiation with indirect dependencies

Suppose that f is a function of two variables, x and y. Normally these variables are assumed to be independent. However, in some situations they may be dependent on each other. For example y could be a function of x, constraining the domain of f to a curve in 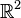$\mathbb{R}^2$ . In this case the partial derivative of f with respect to x does not give the true rate of change of f with respect to changing x because changing x necessarily changes y. The total derivative takes such dependencies into account.

For example, suppose

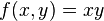f(x,y)=xy

The rate of change of f with respect to x is usually the partial derivative of f with respect to x; in this case,

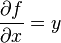\frac{\partial f}{\partial x} = y

However, if y depends on x, the partial derivative does not give the true rate of change of f as x changes because it holds y fixed.

Suppose we are constrained to the line

y=x;

then

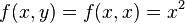f(x,y) = f(x,x) = x^2

In that case, the total derivative of f with respect to x is

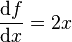\frac{\mathrm{d}f}{\mathrm{d}x} = 2 x

Instead of immediately substituting for y in terms of x, this can be found equivalently using the chain rule:

\frac{\mathrm{d}f}{\mathrm{d}x}= \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}x} = y+x \cdot 1 = x+y.

Notice that this is not equal to the partial derivative:

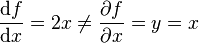\frac{\mathrm{d}f}{\mathrm{d}x} = 2 x \neq \frac{\partial f}{\partial x} = y = x

While one can often perform substitutions to eliminate indirect dependencies, the chain rule provides for a more efficient and general technique. Suppose M(t, p₁, ..., p_n) is a function of time t and n variables 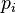$p_i$ which themselves depend on time. Then, the total time derivative of M is

{\operatorname{d}M \over \operatorname{d}t} = \frac{\operatorname d}{\operatorname d t} M \bigl(t, p_1(t), \ldots, p_n(t)\bigr).

The chain rule for differentiating a function of several variables implies that

{\operatorname{d}M \over \operatorname{d}t} = \frac{\partial M}{\partial t} + \sum_{i=1}^n \frac{\partial M}{\partial p_i}\frac{\operatorname{d}p_i}{\operatorname{d}t} = \biggl(\frac{\partial}{\partial t} + \sum_{i=1}^n \frac{\operatorname{d}p_i}{\operatorname{d}t}\frac{\partial}{\partial p_i}\biggr)(M).

This expression is often used in physics for a gauge transformation of the Lagrangian, as two Lagrangians that differ only by the total time derivative of a function of time and the n generalized coordinates lead to the same equations of motion. An interesting example concerns the resolution of causality concerning the Wheeler–Feynman time-symmetric theory. The operator in brackets (in the final expression) is also called the total derivative operator (with respect to t).

For example, the total derivative of f(x(t), y(t)) is

\frac{\operatorname df}{\operatorname dt} = { \partial f \over \partial x}{\operatorname dx \over \operatorname dt }+{ \partial f \over \partial y}{\operatorname dy \over \operatorname dt }.

Here there is no ∂f / ∂t term since f itself does not depend on the independent variable t directly.

The total derivative via differentials

Differentials provide a simple way to understand the total derivative. For instance, suppose 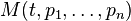$M(t,p_1,\dots,p_n)$ is a function of time t and n variables 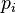$p_i$ as in the previous section. Then, the differential of M is

\operatorname d M = \frac{\partial M}{\partial t} \operatorname d t + \sum_{i=1}^n \frac{\partial M}{\partial p_i}\operatorname{d}p_i.

This expression is often interpreted heuristically as a relation between infinitesimals. However, if the variables t and 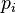$p_i$ are interpreted as functions, and 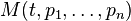$M(t,p_1,\dots,p_n)$ is interpreted to mean the composite of M with these functions, then the above expression makes perfect sense as an equality of differential 1-forms, and is immediate from the chain rule for the exterior derivative. The advantage of this point of view is that it takes into account arbitrary dependencies between the variables. 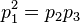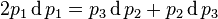For example, if $p_1^2=p_2 p_3$ then $2p_1\operatorname dp_1=p_3 \operatorname d p_2+p_2\operatorname d p_3$ . In particular, if the variables 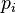$p_i$ are all functions of t, as in the previous section, then

\operatorname d M = \frac{\partial M}{\partial t} \operatorname d t + \sum_{i=1}^n \frac{\partial M}{\partial p_i}\frac{\partial p_i}{\partial t}\,\operatorname d t.

The total derivative as a linear map

Let 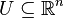$U\subseteq \mathbb{R}^{n}$ be an open subset. Then a function 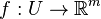$f:U\rightarrow \mathbb{R}^m$ is said to be (totally) differentiable at a point 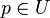$p\in U$ , if there exists a linear map 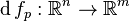$\operatorname df_p:\mathbb{R}^n \rightarrow \mathbb{R}^m$ (also denoted D_pf or Df(p)) such that

\lim_{x\rightarrow p}\frac{\|f(x)-f(p)-\operatorname df_p(x-p)\|}{\|x-p\|}=0.

The linear map 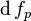$\operatorname d f_p$ is called the (total) derivative or (total) differential of $f$ at $p$ . A function is (totally) differentiable if its total derivative exists at every point in its domain.

Note that f is differentiable if and only if each of its components 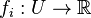$f_i:U\rightarrow \mathbb{R}$ is differentiable. For this it is necessary, but not sufficient, that the partial derivatives of each function f_j exist. However, if these partial derivatives exist and are continuous, then f is differentiable and its differential at any point is the linear map determined by the Jacobian matrix of partial derivatives at that point.

Total differential equation

A total differential equation is a differential equation expressed in terms of total derivatives. Since the exterior derivative is a natural operator, in a sense that can be given a technical meaning, such equations are intrinsic and geometric.

Application of the total differential to error estimation

In measurement, the total differential is used in estimating the error Δf of a function f based on the errors Δx, Δy, ... of the parameters x, y, .... Assuming that the interval is short enough for the change to be approximately linear:

Δf(x) = f'(x) × Δx

and that all variables are independent, then for all variables,

\Delta f = f_x \Delta x + f_y \Delta y + \cdots

This is because the derivative f_x with respect to the particular parameter x gives the sensitivity of the function f to a change in x, in particular the error Δx. As they are assumed to be independent, the analysis describes the worst-case scenario. The absolute values of the component errors are used, because after simple computation, the derivative may have a negative sign. From this principle the error rules of summation, multiplication etc. are derived, e.g.:

Let f(a, b) = a × b;

Δf = f_aΔa + f_bΔb; evaluating the derivatives

Δf = bΔa + aΔb; dividing by f, which is a × b

Δf/f = Δa/a + Δb/b

That is to say, in multiplication, the total relative error is the sum of the relative errors of the parameters.

To illustrate how this depends on the function considered, consider the case where the function is f(a, b) = a ln b instead. Then, it can be computed that the error estimate is

Δf/f = Δa/a + Δb/(b ln b)

with an extra 'ln b' factor not found in the case of a simple product. This additional factor tends to make the error smaller, as ln b is not as large as a bare b.

References

↑ Chiang, Alpha C. Fundamental Methods of Mathematical Economics, McGraw-Hill, third edition, 1984.

A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition), Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2
From thesaurus.maths.org total derivative