Torsor (algebraic geometry)
In algebraic geometry, given a smooth algebraic group G, a G-torsor or a principal G-bundle P over a scheme X is a scheme (or even algebraic space) with the action of G that is locally trivial in the given Grothendieck topology in the sense that the base change 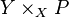 along "some" covering map
along "some" covering map 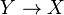 is the trivial torsor
is the trivial torsor 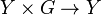 (G acts only on the second factor).[1] Equivalently, a G-torsor P on X is a principal homogeneous space for the group scheme
(G acts only on the second factor).[1] Equivalently, a G-torsor P on X is a principal homogeneous space for the group scheme 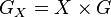 (i.e.,
(i.e., 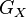 acts simply transitively on
acts simply transitively on  .)
.)
The definition may be formulated in the sheaf-theoretic language: a sheaf P on the category of X-schemes with some Grothendieck topology is a G-torsor if there is a covering  in the topology, called the local trivialization, such that the restriction of P to each
in the topology, called the local trivialization, such that the restriction of P to each 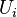 is a trivial
is a trivial 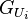 -torsor.
-torsor.
A line bundle is nothing but a 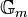 -bundle, and, like a line bundle, the two points of views of torsors, geometric and sheaf-theoretic, are used interchangeably (by permitting P to be a stack like an algebraic space if necessary[2]).
-bundle, and, like a line bundle, the two points of views of torsors, geometric and sheaf-theoretic, are used interchangeably (by permitting P to be a stack like an algebraic space if necessary[2]).
Examples and basic properties
Examples
- A
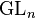 -torsor on X is a vector bundle of rank n (i.e., a locally free sheaf) on X.
-torsor on X is a vector bundle of rank n (i.e., a locally free sheaf) on X. - If
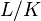 is a finite Galois extension, then
is a finite Galois extension, then 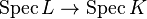 is a
is a 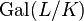 -torsor (roughly because the Galois group acts simply transitively on the roots.) This fact is a basis for Galois descent. See integral extension for a generalization.
-torsor (roughly because the Galois group acts simply transitively on the roots.) This fact is a basis for Galois descent. See integral extension for a generalization.
Remark: A G-torsor P over X is isomorphic to a trivial torsor if and only if 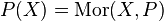 is nonempty. (Proof: if there is an
is nonempty. (Proof: if there is an 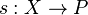 , then
, then 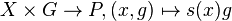 is an isomorphism.)
is an isomorphism.)
Let P be a G-torsor with a local trivialization  in étale topology. A trivial torsor admits a section: thus, there are elements
in étale topology. A trivial torsor admits a section: thus, there are elements 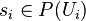 . Fixing such sections
. Fixing such sections 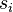 , we can write uniquely
, we can write uniquely 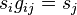 on
on 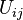 with
with 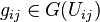 . Different choices of
. Different choices of 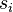 amount to 1-coboundaries in cohomology; that is, the
amount to 1-coboundaries in cohomology; that is, the 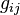 define a cohomology class in the sheaf cohomology (more precisely Čech cohomology with sheaf coefficient) group
define a cohomology class in the sheaf cohomology (more precisely Čech cohomology with sheaf coefficient) group 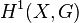 .[3] A trivial torsor corresponds to the identity element. Conversely, it is easy to see any class in
.[3] A trivial torsor corresponds to the identity element. Conversely, it is easy to see any class in 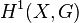 defines a G-torsor on X, unique up to an isomorphism.
defines a G-torsor on X, unique up to an isomorphism.
If G is a connected algebraic group over a finite field 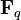 , then any G-bundle over
, then any G-bundle over 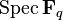 is canonical. (Lang's theorem.)
is canonical. (Lang's theorem.)
Reduction of a structure group
Most of constructions and terminology regarding principal bundles in algebraic topology carry over in verbatim to G-bundles. For example, if 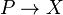 is a G-bundle and G acts from the left on a scheme F, then one can form the associated bundle
is a G-bundle and G acts from the left on a scheme F, then one can form the associated bundle 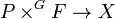 with fiber F. In particular, if H is a closed subgroup of G, then for any H-bundle P,
with fiber F. In particular, if H is a closed subgroup of G, then for any H-bundle P, 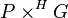 is a G-bundle called the induced bundle.
is a G-bundle called the induced bundle.
If P is a G-bundle that is isomorphic to the induced bundle 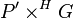 for some H-bundle P', then P is said to admit a reduction of structure group from G to H.
for some H-bundle P', then P is said to admit a reduction of structure group from G to H.
Let X be a smooth projective curve over an algebraically closed field k, G a semisimple algebraic group and P a G-bundle on a relative curve 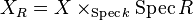 , R a finitely generated k-algebra. Then a theorem of Drinfeld and Simpson states that, if G is simply connected and split, there is an étale morphism
, R a finitely generated k-algebra. Then a theorem of Drinfeld and Simpson states that, if G is simply connected and split, there is an étale morphism 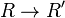 such that
such that 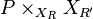 admits a reduction of structure group to a Borel subgroup of G.[4][5]
admits a reduction of structure group to a Borel subgroup of G.[4][5]
Invariants
If P is a parabolic subgroup of a smooth affine group scheme G with connected fibers, then its degree of instability, denoted by 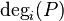 , is the degree of its Lie algebra
, is the degree of its Lie algebra 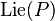 as a vector bundle on X. The degree of instability of G is then
as a vector bundle on X. The degree of instability of G is then 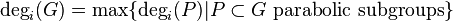 . If G is an algebraic group and E is a G-torsor, then the degree of instability of E is the degree of the inner form
. If G is an algebraic group and E is a G-torsor, then the degree of instability of E is the degree of the inner form 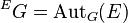 of G induced by E (which is a group scheme over X); i.e.,
of G induced by E (which is a group scheme over X); i.e., 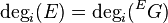 . E is said to be semi-stable if
. E is said to be semi-stable if 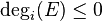 and is stable if
and is stable if 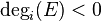 .
.
See also
Notes
- ↑ Algebraic stacks, Example 2.3.
- ↑ Behrend 1993, Lemma 4.3.1
- ↑ Milne 1980, The discussion preceding Proposition 4.6.
- ↑ http://www.math.harvard.edu/~gaitsgde/grad_2009/SeminarNotes/Oct27(Higgs).pdf
- ↑ http://www.math.harvard.edu/~lurie/282ynotes/LectureXIV-Borel.pdf
References
- Behrend, K. The Lefschetz Trace Formula for the Moduli Stack of Principal Bundles. PhD dissertation.
- Behrend, Kai; Conrad, Brian; Edidin, Dan; Fulton, William; Fantechi, Barbara; Göttsche, Lothar; Kresch, Andrew (2006), Algebraic stacks
- Milne, James S. (1980), Étale cohomology, Princeton Mathematical Series 33, Princeton University Press, ISBN 978-0-691-08238-7, MR 559531