Torsion coefficient (topology)
In topology, a mathematical discipline, a torsion coefficient originated as an invariant characteristic of a manifold or hyper-surface. It is a measure of the degree of inherent twist or torsion in the manifold. Torsion coefficients were introduced with the theory of homology by the French mathematician Henri Poincaré around 1900.[1] Since then, homology and its torsion coefficients have found applications elsewhere.
Topological invariants
The Betti numbers and torsion coefficients for a manifold are topological invariants which fully characterise its topology. Manifolds may be broadly divided into those with and without torsion.[2] Where the Euler characteristic and orientability traditionally characterise a two-dimensional manifold, the Betti numbers and torsion coefficients may be understood as more sophisticated generalisations respectively of the Euler value and orientability.
| Manifold | Orientability | Betti numbers | Torsion coefficient (1-dimensional) | ||
|---|---|---|---|---|---|
| b0 | b1 | b2 | |||
| Sphere | Orientable | 1 | 0 | 1 | none |
| Torus | Orientable | 1 | 2 | 1 | none |
| 2-holed torus | Orientable | 1 | 4 | 1 | none |
| g-holed torus | Orientable | 1 | 2g | 1 | none |
| Klein bottle | Non-orientable | 1 | 1 | 0 | 2 |
| Projective plane | Non-orientable | 1 | 0 | 0 | 2 |
| Sphere with c cross-caps | Non-orientable | 1 | c − 1 | 0 | 2 |
Derivation
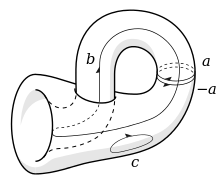
A torsion coefficient is broadly similar in derivation to a Betti number, except that it characterises a non-orientable aspect of a manifold. Accordingly, the arithmetic for manipulating torsion coefficients differs slightly from that for Betti numbers.[3]
A simple understanding can be obtained using oriented loops or cycles on a surface (two-dimensional manifold). In this context, oriented means that a cycle, shown as a in the diagram, follows the loop round in a particular direction. Following the loop round in the opposite direction gives cycle −a.
In homology, a manifold is characterised by the number and types of irreducible cycles on it, which cannot be morphed into each other by smooth deformations.
Cycles which cross, say a and b, may be added together to create a new cycle, d ≡ a + b. Clearly, d may be reduced to a + b.
If you follow a loop round and then back again, you have gone nowhere, so a + (−a) ≡ 0
A simple loop, shown as c in the diagram, which can be shrunk or reduced to a point also has value 0.
On an orientable manifold, such as a torus, following round a non-zero cycle twice gives a non-zero result, i.e. a + a ≡ 2a. Counting the cycles which cannot be deformed into each other is the origin of Betti numbers.
But on a non-orientable manifold such as the Klein bottle, following certain non-zero cycles round twice, as 2a, gives a zero result. For example on the projective plane an oriented line forms a non-zero cycle which cannot be shrunk, while traversing the line twice forms a shrinkable loop, which is zero, i.e. a + a ≡ 0. Counting these multiple traversals is the origin of torsion coefficients.
Therefore, whether or not a surface has a torsion coefficient indicates whether it is orientable or not.
The value of a 1-dimesional torsion coefficient gives the number of times which a loop must be followed round in order to become a zero cycle.[3]
In one form of topological analysis, this is expressed as the number of times which a closed 1-chain must be traversed in order to bound a certain 2-chain.[4]
Citations
Notes
- ↑ Erhard Scholz (Ed. I.M. James, 1999), Page 45: "In the end Poincaré had achieved a lot for a homological theory of (differentiable compact) manifolds about the turn of the century. He had introduced the old invariants (Betti numbers) in a new, much clearer symbolical framework, had introduced new ones (torsion coefficients)..."
- ↑ Erhard Scholz (Ed. I.M. James 1999), page 45: "Poincare (1900) presented a new definition and a calculus for the calculation of Betti numbers and torsion coefficients.... That allowed him to read off immediately the Betti numbers and torsion coefficients and the distinction between manifolds 'with' or 'without' torsion...."
- ↑ 3.0 3.1 3.2 Richeson (2008)
- ↑ Seifert & Threlfall, Page 220.