Torsion-free abelian group
| Algebraic structure → Group theory Group theory |
|---|
|
Modular groups
|
Infinite dimensional Lie group
|
In mathematics, specifically in abstract algebra, a torsion-free abelian group is an abelian group which has no non-trivial torsion elements; that is, a group in which the group operation is commutative and the identity element is the only element with finite order. That is, multiples of any element other than the identity element generate an infinite number of distinct elements of the group.
Definitions
Main article: Abelian group
An abelian group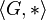 
is a set G, together with a binary operation * on G, such that the following axioms are satisfied:
- Associativity
- For all a, b and c in G, (a * b) *c = a * (b * c).
- Identity element
- There is an element e in G, such that e * x = x * e = x for all x in G. This element e is an identity element for * on G.
- Inverse element
- For each a in G, there is an element a′ in G with the property that a′ * a = a * a′ = e. The element a′ is an inverse of a with respect to *.
- Commutativity
- For all a, b in G, a * b = b * a.[1][2][3]
Main article: Order (group theory)
- Order
- For this definition, note that in an abelian group, the binary operation is usually called addition, the symbol for addition is “+”[4] and a repeated sum,
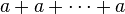of the same element appearing n times is usually abbreviated “na”.[5] Let G be a group and a ∈ G. If there is a positive integer n such that na = e, the least such positive integer n is the order of a. If no such n exists, then a is of infinite order.[6][7][8]
Main article: Torsion (algebra)
- Torsion
- A group G is a torsion group if every element in G is of finite order. G is torsion free if no element other than the identity is of finite order.[9][10][11]
Properties
- A torsion-free abelian group has no non-trivial finite subgroups.
- A finitely generated torsion-free abelian group is free.[12]
See also
Notes
- ↑ Fraleigh (1976, pp. 18−20)
- ↑ Herstein (1964, pp. 26−27)
- ↑ McCoy (1968, pp. 143−146)
- ↑ Fraleigh (1976, p. 27)
- ↑ Fraleigh (1976, p. 30)
- ↑ Fraleigh (1976, pp. 50,72)
- ↑ Herstein (1964, p. 37)
- ↑ McCoy (1968, p. 166)
- ↑ Fraleigh (1976, p. 78)
- ↑ Lang (2002, p. 42)
- ↑ Hungerford (1974, p. 78)
- ↑ Lang (2002, p. 45)
References
- Fraleigh, John B. (1976), A First Course In Abstract Algebra (2nd ed.), Reading: Addison-Wesley, ISBN 0-201-01984-1
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Hungerford, Thomas W. (1974), Algebra, New York: Springer-Verlag, ISBN 0-387-90518-9.
- Lang, Serge (2002), Algebra (Revised 3rd ed.), New York: Springer-Verlag, ISBN 0-387-95385-X.
- McCoy, Neal H. (1968), Introduction To Modern Algebra, Revised Edition, Boston: Allyn and Bacon, LCCN 68-15225
| ||||||||||||||||||||||||||