Topological category
In category theory, a discipline in mathematics, the notion of topological category has a number of different, inequivalent definitions.
In one approach, a topological category is a category that is enriched over the category of compactly generated Hausdorff spaces. They can be used as a foundation for higher category theory, where they can play the role of (∞,1)-categories. An important example of a topological category in this sense is given by the category of CW complexes, where each set Hom(X,Y) of continuous maps from X to Y is equipped with the compact-open topology. (Lurie 2009)
In another approach, a topological category is defined as a category  along with a forgetful functor
along with a forgetful functor 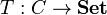 that maps to the category of sets and has the following three properties:
that maps to the category of sets and has the following three properties:
-
 admits initial (or weak) structures with respect to
admits initial (or weak) structures with respect to 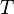
- Constant functions in
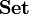 lift to
lift to  -morphisms
-morphisms - Fibers
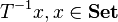 are small (they are sets and not proper classes).
are small (they are sets and not proper classes).
An example of a topological category in this sense is the categories of all topological spaces with continuous maps, where one uses the standard forgetful functor.[1]
See also
- Infinity category
- Simplicial category
References
- ↑ Brümmer, G. C. L. (September 1984). "Topological categories". Topology and its Applications 18 (1): 27–41. doi:10.1016/0166-8641(84)90029-4. Retrieved 1 October 2013.
- Lurie, Jacob (2009), Higher topos theory, Annals of Mathematics Studies 170, Princeton University Press, arXiv:math.CT/0608040, ISBN 978-0-691-14049-0, MR 2522659