Top-hat transform

In mathematical morphology and digital image processing, top-hat transform is an operation that extracts small elements and details from given images. There exist two types of top-hat transform: The white top-hat transform is defined as the difference between the input image and its opening by some structuring element; The black top-hat transform is defined dually as the difference between the closing and the input image. Top-hat transforms are used for various image processing tasks, such as feature extraction, background equalization, image enhancement, and others.

Mathematical definitions

Let 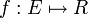$f:E\mapsto R$ be a grayscale image, mapping points from an Euclidean space or discrete grid E (such as R² or Z²) into the real line. Let 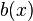$b(x)$ be a grayscale structuring element.

Then, the white top-hat transform of f is given by:

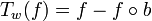T_w(f)=f-f \circ b

where $\circ$ denotes the opening operation.

The black top-hat transform of f (sometimes called the bottom-hat transform^[1] ) is given by:

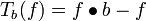T_b(f)=f\bullet b-f

where $\bullet$ is the closing operation.

Properties

The white top-hat transform returns an image, containing those "objects" or "elements" of an input image that:

Are "smaller" than the structuring element (i.e., places where the structuring element does not fit in), and
are brighter than their surroundings.

The black top-hat returns an image, containing the "objects" or "elements" that:

Are "smaller" than the structuring element, and
are darker than their surroundings.

The size, or width, of the elements that are extracted by the top-hat transforms can be controlled by the choice of the structuring element $b$ . The bigger the latter, the larger the elements extracted.

Both top-hat transforms are images that contain only non-negative values at all pixels.

References

Image Analysis and Mathematical Morphology by Jean Serra, ISBN 0-12-637240-3 (1982)
Image Analysis and Mathematical Morphology, Volume 2: Theoretical Advances by Jean Serra, ISBN 0-12-637241-1 (1988)
An Introduction to Morphological Image Processing by Edward R. Dougherty, ISBN 0-8194-0845-X (1992)
Hands-on Morphological Image Processing by Edward R. Dougherty and R. Lotufo, ISBN 0-8194-4720-X (2003)

↑ Tcheslavski, Gleb V. (2010). "Morphological Image Processing: Gray-scale morphology". Retrieved 4 November 2013.