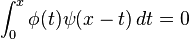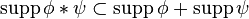Titchmarsh convolution theorem

The Titchmarsh convolution theorem is named after Edward Charles Titchmarsh, a British mathematician. The theorem describes the properties of the support of the convolution of two functions.

Titchmarsh convolution theorem

E.C. Titchmarsh proved the following theorem in 1926:

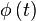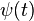If \phi\,(t) and \psi(t)\, are integrable functions, such that
\int_{0}^{x}\phi(t)\psi(x-t)\,dt=0
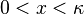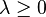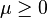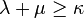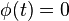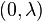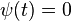almost everywhere in the interval 0<x<\kappa\,, then there exist \lambda\geq0 and \mu\geq0 satisfying \lambda+\mu\ge\kappa such that \phi(t)=0\, almost everywhere in (0,\lambda)\,, and \psi(t)=0\, almost everywhere in (0,\mu)\,.

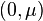This result, known as the Titchmarsh convolution theorem, could be restated in the following form:

Let 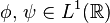\phi,\,\psi\in L^1(\mathbb{R}). Then 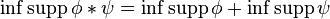\inf\mathop{\rm supp}\,\phi\ast \psi =\inf\mathop{\rm supp}\,\phi+\inf\mathop{\rm supp}\,\psi if the right-hand side is finite.
Similarly, 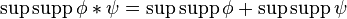\sup\mathop{\rm supp}\,\phi\ast\psi=\sup\mathop{\rm supp}\,\phi+\sup\mathop{\rm supp}\,\psi if the right-hand side is finite.

This theorem essentially states that the well-known inclusion

{\rm supp}\,\phi\ast \psi \subset \mathop{\rm supp}\,\phi +\mathop{\rm supp}\,\psi

is sharp at the boundary.

The higher-dimensional generalization in terms of the convex hull of the supports was proved by J.-L. Lions in 1951:

If 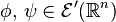\phi,\,\psi\in\mathcal{E}'(\mathbb{R}^n), then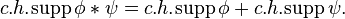 \mathop{c.h.}\mathop{\rm supp}\,\phi\ast \psi=\mathop{c.h.}\mathop{\rm supp}\,\phi+\mathop{c.h.}\mathop{\rm supp}\,\psi.

Above, 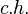\mathop{c.h.} denotes the convex hull of the set. 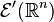\mathcal{E}'(\mathbb{R}^n) denotes the space of distributions with compact support.

The theorem lacks an elementary proof. The original proof by Titchmarsh is based on the Phragmén–Lindelöf principle, Jensen's inequality, Theorem of Carleman, and Theorem of Valiron. More proofs are contained in [Hörmander, Theorem 4.3.3] (harmonic analysis style), [Yosida, Chapter VI] (real analysis style), and [Levin, Lecture 16] (complex analysis style).

References