Tilted large deviation principle
In mathematics — specifically, in large deviations theory — the tilted large deviation principle is a result that allows one to generate a new large deviation principle from an old one by "tilting", i.e. integration against an exponential functional. It can be seen as an alternative formulation of Varadhan's lemma.
Statement of the theorem
Let X be a Polish space (i.e., a separable, completely metrizable topological space), and let (με)ε>0 be a family of probability measures on X that satisfies the large deviation principle with rate function I : X → [0, +∞]. Let F : X → R be a continuous function that is bounded from above. For each Borel set S ⊆ X, let
and define a new family of probability measures (νε)ε>0 on X by
Then (νε)ε>0 satisfies the large deviation principle on X with rate function IF : X → [0, +∞] given by
References
- den Hollander, Frank (2000). Large deviations. Fields Institute Monographs 14. Providence, RI: American Mathematical Society. pp. x+143. ISBN 0-8218-1989-5. MR 1739680
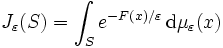
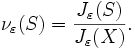
![I^{F} (x) = \sup_{y \in X} \big[ F(y) - I(y) \big] - \big[ F(x) - I(x) \big].](../I/m/3ab40e16ff3d459ab4b0ff1cb338a118.png)