Three subgroups lemma
In mathematics, more specifically group theory, the three subgroups lemma is a result concerning commutators. It is a consequence of the Hall–Witt identity.
Notation
In that which follows, the following notation will be employed:
- If H and K are subgroups of a group G, the commutator of H and K will be denoted by [H,K]; if L is a third subgroup, the convention that [H,K,L] = [[H,K],L] will be followed.
- If x and y are elements of a group G, the conjugate of x by y will be denoted by
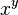 .
. - If H is a subgroup of a group G, then the centralizer of H in G will be denoted by CG(H).
Statement
Let X, Y and Z be subgroups of a group G, and assume
![[X,Y,Z]=1](../I/m/73ea984cd6f46d5a6d72fc4fb47b56e1.png) and
and ![[Y,Z,X]=1](../I/m/49f351828e487847299b11a996c7c27f.png)
Then ![[Z,X,Y]=1](../I/m/4c025f264775b78c5562d27a37347f70.png) .[1]
.[1]
More generally, if 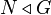 , then if
, then if ![[X,Y,Z]\subseteq N](../I/m/3edbb42f20dfef410321710b1d27bf12.png) and
and ![[Y,Z,X]\subseteq N](../I/m/34ad456387dac60a79e04c7ba06cb798.png) , then
, then ![[Z,X,Y]\subseteq N](../I/m/8b4b62ab8f8ed35dfa7f422755a38b50.png) .[2]
.[2]
Proof and the Hall–Witt identity
Hall–Witt identity
If 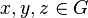 , then
, then
![[x, y^{-1}, z]^y\cdot[y, z^{-1}, x]^z\cdot[z, x^{-1}, y]^x = 1](../I/m/59da6b592baaf8dbdccad69e7a3e224e.png)
Proof of the Three subgroups lemma
Let 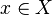 ,
, 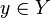 , and
, and 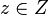 . Then
. Then ![[x,y^{-1},z]=1=[y,z^{-1},x]](../I/m/c9517ce2cecbd2b81dfdc2af3fb4eba6.png) , and by the Hall–Witt identity above, it follows that
, and by the Hall–Witt identity above, it follows that ![[z,x^{-1},y]^{x}=1](../I/m/08c9b16dee8472dadeadd2380fdbb0e7.png) and so
and so ![[z,x^{-1},y]=1](../I/m/d824cff9a17c8ce7a070e25e92f654db.png) . Therefore,
. Therefore, ![[z,x^{-1}]\subseteq \bold{C}_G(Y)](../I/m/0d89523a18930b44a7cdf452e45a76d2.png) for all
for all 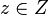 and
and 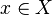 . Since these elements generate
. Since these elements generate ![[Z,X]](../I/m/6e643ef9d5ed52970f589c63b3e42540.png) , we conclude that
, we conclude that ![[Z,X]\subseteq \bold{C}_G(Y)](../I/m/7097d6c77fd01b3ddea4455d780f8226.png) and hence
and hence ![[Z,X,Y]=1](../I/m/4c025f264775b78c5562d27a37347f70.png) .
.
See also
- Commutator
- Lower central series
- Grün's lemma
Notes
References
- I. Martin Isaacs (1993). Algebra, a graduate course (1st edition ed.). Brooks/Cole Publishing Company. ISBN 0-534-19002-2.