Three-center four-electron bond

The 3-center 4-electron bond is a model used to explain bonding in certain hypervalent molecules such as tetratomic and hexatomic interhalogen compounds, sulfur tetrafluoride, the xenon fluorides, and the bifluoride ion.[1][2] It is also known as the Pimentel–Rundle three-center model after the work published by George C. Pimentel in 1951,[3] which built on concepts developed earlier by Robert E. Rundle for electron-deficient bonding.[4] An extended version of this model is used to describe the whole class of hypervalent molecules such as phosphorus pentafluoride and sulfur hexafluoride as well as multi-center pi-bonding such as ozone and sulfur trioxide.

Description

Molecular orbital theory

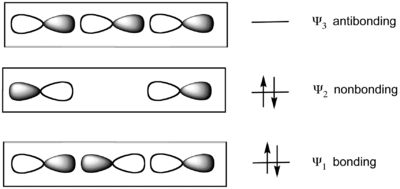
The model considers bonding of three colinear atoms. For example in xenon difluoride (XeF2), the linear F−Xe−F unit is described by a set of three molecular orbitals (MOs) derived from colinear p-orbitals on each atom. The Xe−F bonds result from the combination of a filled p orbital in the central atom (Xe) with two half-filled p orbitals on the axial atoms (F), resulting in a filled bonding orbital, a filled non-bonding orbital, and an empty antibonding orbital. The two lower energy MO's are doubly occupied. The bond order for each Xe-F bonds is 1/2, since the only bonding orbital is delocalized over the two Xe-F bonds.[5]

The HOMO is localized on the two terminal atoms. This localization of charge is accommodated by the fact that the terminal ligands are highly electronegative in hypervalent molecules. The linear F−A−F axis of the molecules SF4 and ClF3 is described as a 3-center 4-electron bond. In the xenon fluorides, all bonds are described with the 3-center 4-electron model. Molecules without an s-orbital lone pair such as PF5 and SF6 are described by an extended version of the 3-center 4-electron model (See hypervalent molecule).

Bonding in the hypervalent molecule XeF2 according to the 3-center 4-electron bond model.

Valence bond theory

The bonding in XeF2 can also be shown qualitatively using resonant Lewis structures as shown below:

\bigg[\ F \frac{\quad}{\quad} Xe^+ \ {}^-\!F \quad \longleftrightarrow \quad F^- \ {}^+\!Xe \frac{\quad}{\quad} F\ \bigg]

In this representation, the octet rule is not broken, the bond orders are 1/2, and there is increased electron density in the fluorine atoms. These results are consistent with the molecular orbital picture discussed above.

Hypervalent description with d orbitals

Older models for explaining hypervalency invoked d orbitals. As of 2010, these models still appear in some beginning-level college texts;[6] however, quantum chemical calculations suggest that d-orbital participation is negligible due to the large energy difference between the relevant p (filled) and d (empty) orbitals. Furthermore, a distinction should be made between "d orbitals" in the valence bond sense and "d functions" that are included in the QM calculation as polarization functions.[7] The 3-center-4-electron bonding model has the advantage of dispensing with the need for d orbitals, which has led to its acceptance.[8]

Other systems

Three-center four-electron interactions can also be considered in the transition state of SN2 reactions and in some (resonant) hydrogen bonding (as in the bifluoride anion):

\bigg[\ F \frac{\quad}{\quad} H\ {}^-\!F \quad \longleftrightarrow \quad F^- \ {}\!H \frac{\quad}{\quad} F\ \bigg]

References

  1. ↑ Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of the Elements (2nd ed.). Butterworth-Heinemann. ISBN 0080379419. p. 897.
  2. ↑ Weinhold, F.; Landis, C. Valency and bonding, Cambridge, 2005; pp. 275-306.
  3. ↑ Pimentel, G. C. The Bonding of Trihalide and Bifluoride Ions by the Molecular Orbital Method. J. Chem. Phys. 1951, 19, 446-448. doi:10.1063/1.1748245
  4. ↑ Rundle, R. E. Electron Deficient Compounds. II. Relative Energies of "Half-Bonds". J. Chem. Phys 1949, 17, 671–675.doi:10.1063/1.1747367
  5. ↑ B.E. Douglas, D.H. McDaniel and J.J. Alexander, Concepts and Models of Inorganic Chemistry, 2nd edition (Wiley 1983) p.164
  6. ↑ New Way Chemistry for Hong Kong A-level, 3rd edition by Manhattan
  7. ↑ E. Magnusson. Hypercoordinate molecules of second-row elements: d functions or d orbitals? J. Am. Chem. Soc. 1990, 112, 7940-7951. doi:10.1021/ja00178a014
  8. ↑ Ramsden, C. A. Non-bonding molecular orbitals and the chemistry of non-classical organic molecules. Chem. Soc. Rev. 1994, 111-118. doi:10.1039/CS9942300111