Thermodynamic integration
Thermodynamic integration is a method used to compare the difference in free energy between two given states (e.g., A and B) whose potential energies 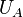 and
and 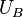 have different dependences on the spatial coordinates. Because the free energy of a system is not simply a function of the phase space coordinates of the system, but is instead a function of the Boltzmann-weighted integral over phase space (i.e. partition function), the free energy difference between two states cannot be calculated directly. In thermodynamic integration, the free energy difference is calculated by defining a thermodynamic path between the states and integrating over ensemble-averaged enthalpy changes along the path. Such paths can either be real chemical processes or alchemical processes. An example alchemical process is the Kirkwood's coupling parameter method.[1]
have different dependences on the spatial coordinates. Because the free energy of a system is not simply a function of the phase space coordinates of the system, but is instead a function of the Boltzmann-weighted integral over phase space (i.e. partition function), the free energy difference between two states cannot be calculated directly. In thermodynamic integration, the free energy difference is calculated by defining a thermodynamic path between the states and integrating over ensemble-averaged enthalpy changes along the path. Such paths can either be real chemical processes or alchemical processes. An example alchemical process is the Kirkwood's coupling parameter method.[1]
Derivation
Consider two systems, A and B, with potential energies 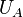 and
and 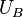 . The potential energy in either system can be calculated as an ensemble average over configurations sampled from a molecular dynamics or Monte Carlo simulation with proper Boltzmann weighting. Now consider a new potential energy function defined as:
. The potential energy in either system can be calculated as an ensemble average over configurations sampled from a molecular dynamics or Monte Carlo simulation with proper Boltzmann weighting. Now consider a new potential energy function defined as:
Here,  is defined as a coupling parameter with a value between 0 and 1, and thus the potential energy as a function of
is defined as a coupling parameter with a value between 0 and 1, and thus the potential energy as a function of  varies from the energy of system A for
varies from the energy of system A for 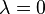 and system B for
and system B for 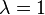 . In the canonical ensemble, the partition function of the system can be written as:
. In the canonical ensemble, the partition function of the system can be written as:
In this notation, 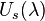 is the potential energy of state
is the potential energy of state  in the ensemble with potential energy function
in the ensemble with potential energy function 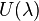 as defined above. The free energy of this system is defined as:
as defined above. The free energy of this system is defined as:
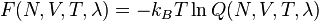 ,
,
If we take the derivative of F with respect to λ, we will get that it equals the ensemble average of the derivative of potential energy with respect to λ.
The change in free energy between states A and B can thus be computed from the integral of the ensemble averaged derivatives of potential energy over the coupling parameter  .[2] In practice, this is performed by defining a potential energy function
.[2] In practice, this is performed by defining a potential energy function 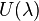 , sampling the ensemble of equilibrium configurations at a series of
, sampling the ensemble of equilibrium configurations at a series of  values, calculating the ensemble-averaged derivative of
values, calculating the ensemble-averaged derivative of 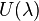 with respect to
with respect to  at each
at each  value, and finally computing the integral over the ensemble-averaged derivatives.
value, and finally computing the integral over the ensemble-averaged derivatives.
Umbrella sampling is a related free energy method. It adds a bias to the potential energy. In the limit of an infinite strong bias it is equivalent to thermodynamic integration.[3]
See also
References
- ↑ J. G. Kirkwood. Statistical mechanics of fluid mixtures, J. Chem. Phys., 3:300-313,1935
- ↑ Frenkel, Daan and Smit, Berend. Understanding Molecular Simulation: From Algorithms to Applications. Academic Press, 2007
- ↑ J Kästner et al. (2006). "QM/MM Free-Energy Perturbation Compared to Thermodynamic Integration and Umbrella Sampling: Application to an Enzymatic Reaction". JCTC 2 (2): 452–461. doi:10.1021/ct050252w.
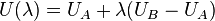
![Q(N, V, T, \lambda) = \sum_{s} \exp [-U_s(\lambda)/k_{B}T]](../I/m/d808824a3ca37a08cd630beba1e1afd7.png)
![\Delta F(A \rightarrow B)
= \int_0^1 d\lambda \frac{\partial F(\lambda)}{\partial\lambda}
= -\int_0^1 d\lambda \frac{k_{B}T}{Q} \frac{\partial Q}{\partial\lambda}
= \int_0^1 d\lambda \frac{k_{B}T}{Q} \sum_{s} \frac{1}{k_{B}T} \exp[- U_s(\lambda)/k_{B}T ] \frac{\partial U_s(\lambda)}{\partial \lambda}
= \int_0^1 d\lambda \left\langle\frac{\partial U(\lambda)}{\partial\lambda}\right\rangle_{\lambda}](../I/m/6ffb83c8f25b73ab97cd96806a631c06.png)