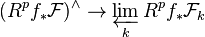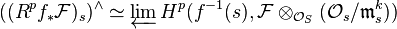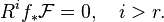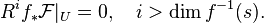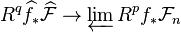Theorem on formal functions

In algebraic geometry, the theorem on formal functions states the following:[1]

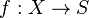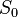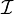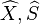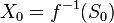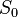Let f: X \to S be a proper morphism of noetherian schemes with a coherent sheaf \mathcal{F} on X. Let S_0 be a closed subscheme of S defined by \mathcal{I} and \widehat{X}, \widehat{S} formal completions with respect to X_0 = f^{-1}(S_0) and S_0. Then for each p \ge 0 the canonical (continuous) map:
(R^p f_* \mathcal{F})^\wedge \to \varprojlim_k R^p f_* \mathcal{F}_k
is an isomorphism of (topological) 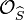\mathcal{O}_{\widehat{S}}-modules, where
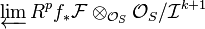  • The left term is \varprojlim R^p f_* \mathcal{F} \otimes_{\mathcal{O}_S} \mathcal{O}_S/{\mathcal{I}^{k+1}}.
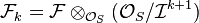
  • \mathcal{F}_k = \mathcal{F} \otimes_{\mathcal{O}_S} (\mathcal{O}_S/{\mathcal{I}}^{k+1})
  • The canonical map is one obtained by passage to limit.

The theorem is used to deduce some other important theorems: Stein factorization and a version of Zariski's main theorem that says that a proper birational morphism into a normal variety is an isomorphism. Some other corollaries (with the notations as above) are:

Corollary:[2] For any 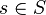s \in S, topologically,

((R^p f_* \mathcal{F})_s)^\wedge \simeq \varprojlim H^p(f^{-1}(s), \mathcal{F}\otimes_{\mathcal{O}_S} (\mathcal{O}_s/\mathfrak{m}_s^k))

where the completion on the left is with respect to 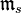\mathfrak{m}_s.

Corollary:[3] Let r be such that 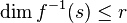\operatorname{dim} f^{-1}(s) \le r for all 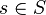s \in S. Then

R^i f_* \mathcal{F} = 0, \quad i > r.

Corollay:[4] For each 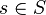s \in S, there exists an open neighborhood U of s such that

R^i f_* \mathcal{F}|_U = 0, \quad i > \operatorname{dim} f^{-1}(s).

Corollary:[5] If 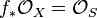f_* \mathcal{O}_X = \mathcal{O}_S, then 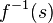f^{-1}(s) is connected for all s \in S.

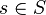The theorem also leads to the Grothendieck existence theorem, which gives an equivalence between the category of coherent sheaves on a scheme and the category of coherent sheaves on its formal completion (in particular, it yields algebralizability.)

Finally, it is possible to weaken the hypothesis in the theorem; cf. Illusie. According to Illusie (pg. 204), the proof given in EGA III is due to Serre. The original proof (due to Grothendieck) was never published.

The construction of the canonical map

Let the setting be as in the lede. In the proof one uses the following alternative definition of the canonical map.

Let 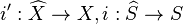i': \widehat{X} \to X, i: \widehat{S} \to S be the canonical maps. Then we have the base change map of 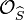\mathcal{O}_{\widehat{S}}-modules

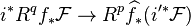i^* R^q f_* \mathcal{F} \to R^p \widehat{f}_* (i'^* \mathcal{F}).

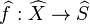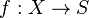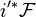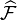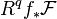where \widehat{f}: \widehat{X} \to \widehat{S} is induced by f: X \to S. Since \mathcal{F} is coherent, we can identify i'^*\mathcal{F} with \widehat{\mathcal{F}}. Since R^q f_* \mathcal{F} is also coherent (as f is proper), doing the same identification, the above reads:

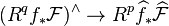(R^q f_* \mathcal{F})^\wedge \to R^p \widehat{f}_* \widehat{\mathcal{F}}.

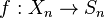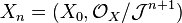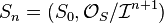Using f: X_n \to S_n where X_n = (X_0, \mathcal{O}_X/\mathcal{J}^{n+1}) and S_n = (S_0, \mathcal{O}_S/\mathcal{I}^{n+1}), one also obtains (after passing to limit):

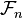R^q \widehat{f}_* \widehat{\mathcal{F}} \to \varprojlim R^p f_* \mathcal{F}_n

where \mathcal{F}_n are as before. One can verify that the composition of the two maps is the same map in the lede. (cf. EGA III-1, section 4)

Notes

  1. ↑ EGA III-1, 4.1.5
  2. ↑ EGA III-1, 4.2.1
  3. ↑ Hartshorne, Ch. III. Corollary 11.2
  4. ↑ The same argument as in the preceding corollary
  5. ↑ Hartshorne, Ch. III. Corollary 11.3

References