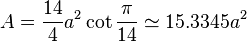Tetradecagon

Regular tetradecagon

A regular tetradecagon
Type Regular polygon
Edges and vertices 14
Schläfli symbol {14}
t{7}
Coxeter diagram
Symmetry group Dihedral (D14), order 2×14
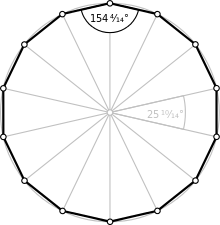
Internal angle (degrees) ≈154.2857°
Dual polygon self
Properties convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a tetradecagon (or tetrakaidecagon) is a polygon with 14 sides and angles.

A regular tetradecagon has Schläfli symbol {14} and can be constructed as a quasiregular truncated heptagon, t{7}, which alternates two types of edges.

Regular tetradecagon

The area of a regular tetradecagon of side length a is given by

A = \frac{14}{4}a^2\cot\frac{\pi}{14}\simeq 15.3345a^2

Numismatic use

The regular tetradecagon is used as the shape of some commemorative gold and silver Malaysian coins, the number of sides representing the 14 states of the Malaysian Federation.[1]

Construction

A regular tetradecagon cannot be constructed using a compass and straightedge.[2] However, it is constructible using neusis, or with an angle trisector. The animation below gives an approximation of about 0.05° on the center angle:


Construction of an approximated regular tetradecagon

Related figures

A tetradecagram is a 14-sided star polygon, represented by symbol {14/n}. There are two regular star polygons: {14/3} and {14/5}, using the same vertices, but connecting every third or fifth points. There are also three compounds: {14/2} is reduced to 2{7} as two heptagons, while {14/4} and {14/6} are reduced to 2{7/2} and 2{7/3} as two different heptagrams, and finally {14/7} is reduced to seven digons.

n1234567
Form Regular Compound Star polygon Compound Star polygon Compound
Image
{14/1} = {14}
{14/2} = 2{7}
{14/3}
{14/4} = 2{7/2}
{14/5}
{14/6} = 2{7/3}
{14/7} or 7{2}
Internal angle ≈154.286° ≈128.571° ≈102.857° ≈77.1429° ≈51.4286° ≈25.7143° 0°

Deeper truncations of the regular heptagon and heptagrams can produce isogonal (vertex-transitive) intermediate tetradecagram forms with equally spaced vertices and two edge lengths. Other truncations can form double covering polyons 2{p/q}, namely: t{7/6}={14/6}=2{7/3}, t{7/4}={14/4}=2{7/2}, and t{7/2}={14/2}=2{7}.[3]

Isogonal truncations of heptagon and heptagrams
Quasiregular Isogonal Quasiregular
Double covering

t{7}={14}
{7/6}={14/6}
=2{7/3}

t{7/3}={14/3}
t{7/4}={14/4}
=2{7/2}

t{7/5}={14/5}
t{7/2}={14/2}
=2{7}

Petrie polygons

Regular skew tetradecagons exist as Petrie polygon for many higher-dimensional polytopes, shown in these skew orthogonal projections, including:

B7 2I2(7) (4D)

7-orthoplex
7-cube
7-7 duopyramid
7-7 duoprism
A13 D8 E8

13-simplex
511
151
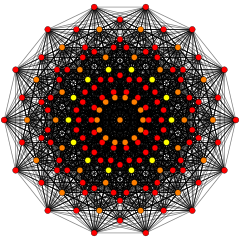421
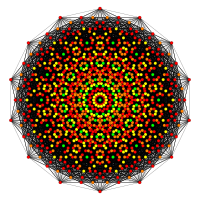241

References

  1. ↑ The Numismatist, Volume 96, Issues 7-12, Page 1409, American Numismatic Association, 1983.
  2. ↑ Wantzel, Pierre (1837). "Recherches sur les moyens de Reconnaître si un Problème de géométrie peau se résoudre avec la règle et le compas". Journal de Mathématiques: 366–372.
  3. ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum

External links