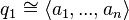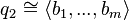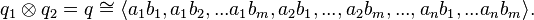Tensor product of quadratic forms

The tensor product of quadratic forms is most easily understood when one views the quadratic forms as quadratic spaces. So, if (V, q₁) and (W, q₂) are quadratic spaces, with V,W vector spaces, then the tensor product is a quadratic form q on the tensor product of vector spaces V ⊗ W.

It is defined in such a way that for 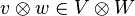$v \otimes w \in V \otimes W$ we have 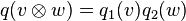$q(v \otimes w) = q_1(v)q_2(w)$ . In particular, if we have diagonalizations of our quadratic forms (which is always possible when the characteristic is not 2) such that

q_1 \cong \langle a_1, ... , a_n \rangle

q_2 \cong \langle b_1, ... , b_m \rangle

then the tensor product has diagonalization

q_1 \otimes q_2 = q \cong \langle a_1b_1, a_1b_2, ... a_1b_m, a_2b_1, ... , a_2b_m , ... , a_nb_1, ... a_nb_m \rangle.