Temperley–Lieb algebra
In statistical mechanics, the Temperley–Lieb algebra is an algebra from which are built certain transfer matrices, invented by Neville Temperley and Elliott Lieb. It is also related to integrable models, knot theory and the braid group, quantum groups and subfactors of von Neumann algebras.
Definition
Let  be a commutative ring and fix
be a commutative ring and fix 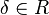 . The Temperley–Lieb algebra
. The Temperley–Lieb algebra 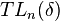 is the
is the  -algebra generated by the elements
-algebra generated by the elements 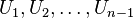 , subject to the Jones relations:
, subject to the Jones relations:
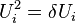 for all
for all 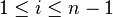
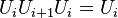 for all
for all 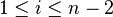
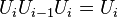 for all
for all 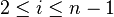
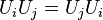 for all
for all 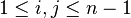 such that
such that 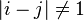
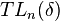 may be represented diagrammatically as the vector space over noncrossing pairings on a rectangle with n points on two opposite sides. The five basis elements of
may be represented diagrammatically as the vector space over noncrossing pairings on a rectangle with n points on two opposite sides. The five basis elements of 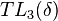 are the following:
are the following:
.svg.png) .
.
Multiplication on basis elements can be performed by placing two rectangles side by side, and replacing any closed loops by a factor of δ, for example:
 ×
× 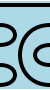 =
= 
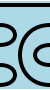 = δ
= δ  .
.
The identity element is the diagram in which each point is connected to the one directly across the rectangle from it, and the generator 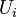 is the diagram in which the ith point is connected to the i+1th point, the 2n − i + 1th point is connected to the 2n − ith point, and all other points are connected to the point directly across the rectangle. The generators of
is the diagram in which the ith point is connected to the i+1th point, the 2n − i + 1th point is connected to the 2n − ith point, and all other points are connected to the point directly across the rectangle. The generators of 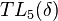 are:
are:
.svg.png)
From left to right, the unit 1 and the generators U1, U2, U3, U4.
The Jones relations can be seen graphically:

 = δ
= δ 


 =
= 

 =
= 

The Temperley-Lieb Hamiltonian
Consider an interaction-round-a-face model e.g. a square lattice model and let  be the number of sites on the lattice. Following Temperley and Lieb[1] we define the Temperley-Lieb hamiltonian (the TL hamiltonian) as
be the number of sites on the lattice. Following Temperley and Lieb[1] we define the Temperley-Lieb hamiltonian (the TL hamiltonian) as
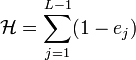
where 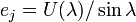 , for some spectral parameter
, for some spectral parameter 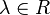 .
.
Applications
We will firstly consider the case 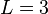 . The TL hamiltonian is
. The TL hamiltonian is 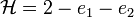 , namely
, namely
 = 2
= 2  -
-  -
-  .
.
We have two possible states,
![]() and
and ![]() .
.
In acting by  on these states, we find
on these states, we find

![]() = 2
= 2 
![]() -
- 
![]() -
- 
![]() =
= ![]() -
- ![]() ,
,
and

![]() = 2
= 2 
![]() -
- 
![]() -
- 
![]() = -
= - ![]() +
+ ![]() .
.
Writing  as a matrix in the basis of possible states we have,
as a matrix in the basis of possible states we have,
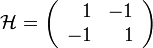
The eigenvector of  with the lowest eigenvalue is known as the ground state. In this case, the lowest eigenvalue
with the lowest eigenvalue is known as the ground state. In this case, the lowest eigenvalue 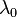 for
for  is
is 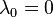 . The corresponding eigenvector is
. The corresponding eigenvector is 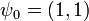 . As we vary the number of sites
. As we vary the number of sites  we find the following table[2]
we find the following table[2]
 |
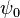 |
 |
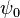 |
|---|---|---|---|
| 2 | (1) | 3 | (1, 1) |
| 4 | (2, 1) | 5 | 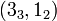 |
| 6 | 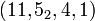 |
7 | 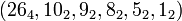 |
| 8 | 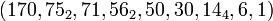 |
9 | 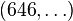 |
 |
 |
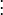 |
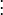 |
where we have use the notation 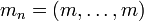
 -times i.e.
-times i.e. 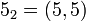 .
.
Combinatorial Properties
An interesting observation is that the largest components of the ground state of  have a combinatorial enumeration as we vary the number of sites,[3] as was first observed by Murray Batchelor, Jan de Gier and Bernard Nienhuis.[2] Using the resources of the on-line encyclopedia of integer sequences, Batchelor et al. found, for an even numbers of sites
have a combinatorial enumeration as we vary the number of sites,[3] as was first observed by Murray Batchelor, Jan de Gier and Bernard Nienhuis.[2] Using the resources of the on-line encyclopedia of integer sequences, Batchelor et al. found, for an even numbers of sites
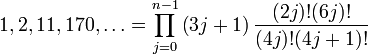
and for an odd numbers of sites
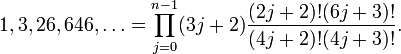
Surprisingly, these sequences corresponded to well known combinatorial objects. For  even, this sequence corresponded to cyclically symmetric transpose complement plane partitions and for
even, this sequence corresponded to cyclically symmetric transpose complement plane partitions and for  odd these corresponded to
odd these corresponded to 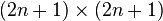 alternating sign matrices symmetric about the vertical axis.
alternating sign matrices symmetric about the vertical axis.
References
- ↑ Temperley N. and Lieb E., (1971), Relations between the 'Percolation' and 'Colouring' Problem and other Graph-Theoretical Problems Associated with Regular Planar Lattices: Some Exact Results for the 'Percolation' Problem, Proc. R. Soc. A 322 251.
- ↑ 2.0 2.1 Batchelor M., de Gier J. and Nienhuis B., (2001), The quantum symmetric
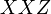 chain at
chain at 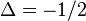 , alternating-sign matrices and plane partitions, J. Phys. A 34, L265-L270.
, alternating-sign matrices and plane partitions, J. Phys. A 34, L265-L270. - ↑ de Gier J., (2005), Loops, matchings and alternating-sign matrices, Discrete Mathematics Volume 298, Issues 1-3, Pages 365-388.
Further reading
- Louis H. Kauffman, State Models and the Jones Polynomial. Topology, 26(3):395-407, 1987.
- R.J. Baxter, Exactly solved models in statistical mechanics Academic Press Inc. (1982)
- N. Temperley, E. Lieb, Relations between the 'Percolation' and 'Colouring' Problem and other Graph-Theoretical Problems Associated with Regular Planar Lattices: Some Exact Results for the 'Percolation' Problem. Proceedings of the Royal Society Series A 322 (1971), 251-280.