Teichmüller–Tukey lemma

In mathematics, the Teichmüller–Tukey lemma (sometimes named just Tukey's lemma,), named after John Tukey and Oswald Teichmüller, states that every nonempty collection of finite character has a maximal element with respect to inclusion. It is equivalent to the Axiom of Choice.

Definitions

A family of sets is of finite character provided it has the following properties:

For each 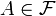$A\in \mathcal{F}$ , every finite subset of $A$ belongs to $\mathcal{F}$ .
If every finite subset of a given set $A$ belongs to $\mathcal{F}$ , then $A$ belongs to $\mathcal{F}$ .

Applications

In linear algebra, the lemma may be used to show the existence of a basis. Let V be a vector space. Consider the collection $\mathcal{F}$ of linearly independent sets of vectors. This is a collection of finite character Thus, a maximal set exists, which must then span V and be a basis for V.

References

Brillinger, David R. "John Wilder Tukey"

Teichmüller–Tukey lemma

Definitions

Applications

See also

References