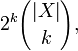Teaching dimension
In computational learning theory, the teaching dimension[1] of a concept class C is defined to be 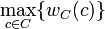 , where
, where 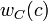 is the minimum size of a witness set for c in C.
is the minimum size of a witness set for c in C.
The teaching dimension of a finite concept class can be used to give a lower and an upper bound on the membership query cost of the concept class.
In Stasys Jukna's book "Extremal Combinatorics", a lower bound is given for the teaching dimension:
Let C be a concept class over a finite domain X. If the size of C is greater than
then the teaching dimension of C is greater than k.
References
- ↑ Sally Goldman and Ronald Rivest and Robert Schapire (1989). "Learning Binary Relations and Total Orders". SIAM J. Computing 22: 46–51.