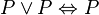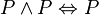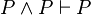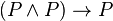Tautology (rule of inference)

Transformation rules
Propositional calculus
Rules of inference
Modus ponens / Modus tollens Biconditional introduction / elimination Conjunction introduction / elimination Disjunction introduction / elimination Disjunctive / Hypothetical syllogism Constructive / Destructive dilemma Absorption Modus ponendo tollens
Rules of replacement
Associativity Commutativity Distributivity Double negation De Morgan's laws Transposition Material implication Exportation Tautology Negation introduction
Predicate logic
Universal generalization / instantiation Existential generalization / instantiation

In propositional logic, tautology is one of two commonly used rules of replacement.^[1]^[2]^[3] The rules are used to eliminate redundancy in disjunctions and conjunctions when they occur in logical proofs. They are:

The principle of idempotency of disjunction:

P \or P \Leftrightarrow P

and the principle of idempotency of conjunction:

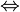P \and P \Leftrightarrow P

Where " $\Leftrightarrow$ " is a metalogical symbol representing "can be replaced in a logical proof with."

Relation to tautology

The rule gets its name from the fact that the concept of the rule is the same as the tautologous statements If "p and p" is true then "p" is true. and If "p or p" is true then "p" is true. This type of tautology is called idempotency. Although the rule is the expression of a particular tautology, this is a bit misleading, as every rule of inference can be expressed as a tautology and vice versa.

Formal notation

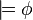Theorems are those logical formulas $\phi$ where $\vdash \phi$ is the conclusion of a valid proof,^[4] while the equivalent semantic consequence $\models \phi$ indicates a tautology.

The tautology rule may be expressed as a sequent:

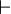P \or P \vdash P \,

and

P \and P \vdash P \,

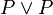where $\vdash$ is a metalogical symbol meaning that $P$ is a syntactic consequence of $P \or P$ , in the one case, 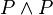$P \and P$ in the other, in some logical system;

or as a rule of inference:

\frac{P \or P}{\therefore P}

and

\frac{P \and P}{\therefore P}

where the rule is that wherever an instance of "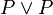 $P \or 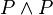P$ " or " $P \and P$ " appears on a line of a proof, it can be replaced with " $P$ ";

or as the statement of a truth-functional tautology or theorem of propositional logic. The principle was stated as a theorem of propositional logic by Russell and Whitehead in Principia Mathematica as:

(P \or P) \to P \,

and

(P \and P) \to P \,

where $P$ is a proposition expressed in some formal system.

References

↑ Hurley, Patrick (1991). A Concise Introduction to Logic 4th edition. Wadsworth Publishing. pp. 364–5.
↑ Copi and Cohen
↑ Moore and Parker
↑ Logic in Computer Science, p. 13