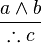Tautological consequence
In propositional logic, tautological consequence is a strict form of logical consequence[1] in which the tautologousness of a proposition is preserved from one line of a proof to the next. Not all logical consequences are tautological consequences. A proposition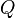 
is said to be a tautological consequence of one or more other propositions (
, 
, ..., 
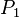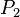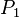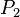) in a proof with respect to some logical system if one is validly able to introduce the proposition onto a line of the proof within the rules of the system and in all cases when each of those one or more other propositions (, , ..., ) are true, the proposition 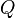also is true.
Another way to express this preservation of tautologousness is by using truth tables. A proposition 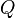is said to be a tautological consequence of one or more other 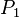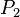propositions (, , ..., ) if and only if in every row of a joint truth table that assigns "T" to all propositions (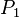, , 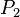..., ) the truth table also assigns "T" to .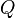
Example
Consider the following argument:
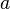= "Socrates is a man."
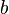= "All men are mortal."
= "Socrates is mortal."
The conclusion of this argument is a logical consequence of the premise because it is impossible for the premise to be true while the conclusion is false.
Now construct a joint truth table.
| a | b | c | a ∧ b | c |
|---|---|---|---|---|
| T | T | T | T | T |
| T | T | F | T | F |
| T | F | T | F | T |
| T | F | F | F | F |
| F | T | T | F | T |
| F | T | F | F | F |
| F | F | T | F | T |
| F | F | F | F | F |
Reviewing the truth table, it turns out the conclusion of the argument is not a tautological consequence of the premise. Not every row that assigns T to the conclusion also assigns T to every proposition in the premise. In particular, it is the second row that assigns T to "a ∧ b," but does not assign T to c.
Denotation and properties
It follows from the definition that if a proposition p is a contradiction then p tautologically implies every proposition, because there is no truth valuation that causes p to be true and so the definition of tautological implication is trivially satisfied. Similarly, if p is a tautology then p is tautologically implied by every proposition.
See also
Notes
- ↑ Barwise and Etchemendy 1999, p. 110
References
- Barwise, Jon, and John Etchemendy. Language, Proof and Logic. Stanford: CSLI (Center for the Study of Language and Information) Publications, 1999. Print.
- Kleene, S. C. (1967) Mathematical Logic, reprinted 2002, Dover Publications, ISBN 0-486-42533-9.