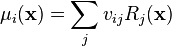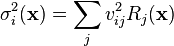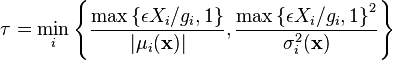Tau-leaping

In probability theory, tau-leaping, or τ-leaping, is an approximate method for the simulation of a stochastic system.^[1] It is based on the Gillespie algorithm, performing all reactions for an interval of length tau before updating the propensity functions.^[2] By updating the rates less often this allows for more efficient simulation and thus the consideration of larger systems.

Cao et al. improved the method to prevent the generation of negative populations.^[3]^[4]

Algorithm

The algorithm is analogous to the Euler method for deterministic systems, but instead of making a fixed change

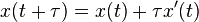
$x(t+\tau)=x(t)+\tau x'(t)$

the change is

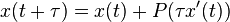
$x(t+\tau)=x(t)+P(\tau x'(t))$

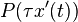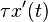where $P(\tau x'(t))$ is a Poisson distributed random variable with mean $\tau x'(t)$ .

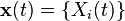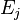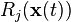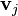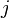Given a state $\mathbf{x}(t)=\{X_i(t)\}$ with events $E_j$ occurring at rate $R_j(\mathbf{x}(t))$ and with state change vectors $\mathbf{v}_j$ (where $i$ indexes the state variables, and $j$ indexes the events), the method is as follows:

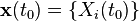Initialise the model with initial conditions $\mathbf{x}(t_0)=\{X_i(t_0)\}$ .
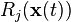Calculate the event rates $R_j(\mathbf{x}(t))$ .
Choose a time step $\tau$ . This may be fixed, or by some algorithm dependent on the various event rates.
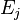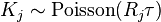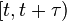For each event $E_j$ generate $K_j \sim \text{Poisson}(R_j\tau)$ , which is the number of times each event occurs during the time interval $[t,t+\tau)$ .
Update the state by
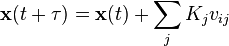
$\mathbf{x}(t+\tau)=\mathbf{x}(t)+\sum_j K_jv_{ij}$

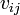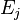where $v_{ij}$ is the change on state variable $X_i$ due to event $E_j$ . At this point it may be necessary to check that no populations have reached unrealistic values (such as a population becoming negative due to the unbounded nature of the Poisson variable $K_j$ ).
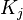Repeat from Step 2 until some desired condition is met (e.g. a particular state variable reaches 0, or time 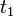$t_1$ is reached).

Algorithm for efficient step size selection

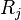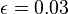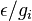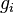This algorithm is described by Cao et al.^[5] The idea is to bound the relative change in each event rate $R_j$ by a specified tolerance $\epsilon$ (Cao et al. recommend $\epsilon=0.03$ , although it may depend on model specifics). 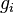This is achieved by bounding the relative change in each state variable $X_i$ by $\epsilon/g_i$ , where $g_i$ depends on the rate that changes the most for a given change in $X_i$ .Typically $g_i$ is equal the highest order event rate, but this may be more complex in different situations (especially epidemiological models with non-linear event rates).

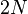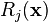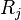This algorithm typically requires computing $2N$ auxiliary values (where $N$ is the number of state variables $X_i$ ), and should only require reusing previously calculated values $R_j(\mathbf{x})$ . An important factor in this since $X_i$ is an integer value, then there is a minimum value by which it can change, preventing the relative change in $R_j$ being bounded by 0, which would result in $\tau$ also tending to 0.

For each state variable $X_i$ , calculate the auxiliary values
$\mu_i(\mathbf{x}) = \sum_j v_{ij} R_j(\mathbf{x})$

$\sigma_i^2(\mathbf{x}) = \sum_j v_{ij}^2 R_j(\mathbf{x})$
For each state variable $X_i$ , determine the highest order event in which it is involved, and obtain $g_i$
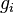
Calculate time step $\tau$ as
$\tau = \min_i {\left\{ \frac{\max{\{\epsilon X_i / g_i, 1\}}}{|\mu_i(\mathbf{x})|}, \frac{\max{\{\epsilon X_i / g_i, 1\}}^2}{\sigma_i^2(\mathbf{x})} \right\}}$

This computed $\tau$ is then used in Step 3 of the $\tau$ leaping algorithm.

References

↑ Gillespie, D. T. (2001). "Approximate accelerated stochastic simulation of chemically reacting systems". The Journal of Chemical Physics 115 (4): 1716–1711. doi:10.1063/1.1378322.
↑ Erhard, F.; Friedel, C. C.; Zimmer, R. (2010). "FERN – Stochastic Simulation and Evaluation of Reaction Networks". Systems Biology for Signaling Networks. p. 751. doi:10.1007/978-1-4419-5797-9_30. ISBN 978-1-4419-5796-2.
↑ Cao, Y.; Gillespie, D. T.; Petzold, L. R. (2005). "Avoiding negative populations in explicit Poisson tau-leaping". The Journal of Chemical Physics 123 (5): 054104. doi:10.1063/1.1992473. PMID 16108628.
↑ Cao, Y.; Gillespie, D. T.; Petzold, L. R. (2006). "Efficient step size selection for the tau-leaping simulation method". The Journal of Chemical Physics 124 (4): 044109. doi:10.1063/1.2159468. PMID 16460151.
↑ Cao, Y.; Gillespie, D. T.; Petzold, L. R. (2006). "Efficient step size selection for the tau-leaping simulation method". The Journal of Chemical Physics 124 (4): 044109. doi:10.1063/1.2159468. PMID 16460151.