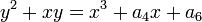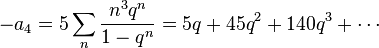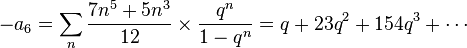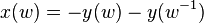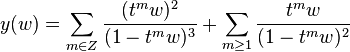Tate curve

In mathematics, the Tate curve is a curve defined over the ring of formal power series $\mathbb{Z}[[q]]$ with integer coefficients. Over the open subscheme where q is invertible, the Tate curve is an elliptic curve. The Tate curve can also be defined for q as an element of a complete field of norm less than 1, in which case the formal power series converge.

The Tate curve was introduced by John Tate (1995) in a 1959 manuscript originally titled "Rational Points on Elliptic Curves Over Complete Fields"; he did not publish his results until many years later, and his work first appeared in Roquette (1970).

Definition

The Tate curve is the projective plane curve over the ring Z[[q]] of formal power series with integer coefficients given (in an affine open subset of the projective plane) by the equation

y^2+xy=x^3+a_4x+a_6

where

-a_4=5\sum_n \frac{n^3q^n}{1-q^n} = 5q+45q^2+140q^3+\cdots

-a_6=\sum_{n}\frac{7n^5+5n^3}{12}\times\frac{q^n}{1-q^n} = q+23q^2+154q^3+\cdots

are power series with integer coefficients.^[1]

The Tate curve over a complete field

Suppose that the field k is complete with respect to some absolute value ||, and q is a non-zero element of the field k with |q|<1. Then the series above all converge, and define an elliptic curve over k. If in addition q is non-zero then there is an isomorphism of groups from k^*/q^Z to this elliptic curve, taking w to (x(w),y(w)) for w not a power of q, where

x(w)= -y(w)-y(w^{-1})

y(w) = \sum_{m\in Z}\frac{(t^mw)^2}{(1-t^mw)^3} + \sum_{m\ge 1} \frac{t^mw}{(1-t^mw)^2}

and taking powers of q to the point at infinity of the elliptic curve. The series x(w) and y(w) are not formal power series in w.

Properties

The j-invariant of the Tate curve is given by a power series in q with leading term q⁻¹.^[2] Over a p-adic local field, therefore, j is non-integral and the Tate curve has semistable reduction of multiplicative type. Conversely, every semistable elliptic curve over a local field is isomorphic to a Tate curve (up to quadratic twist).^[3]

References

↑ Manin & Panchishkin (2007) p.220
↑ Silverman (1994) p.423
↑ Manin & Panchiskin (2007) p.300

Lang, Serge (1987), Elliptic functions, Graduate Texts in Mathematics 112 (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96508-6, MR 890960, Zbl 0615.14018
Manin, Yu. I.; Panchishkin, A. A. (2007). Introduction to Modern Number Theory. Encyclopaedia of Mathematical Sciences 49 (Second ed.). ISBN 978-3-540-20364-3. ISSN 0938-0396. Zbl 1079.11002.
Robert, Alain (1973), Elliptic curves, Lecture Notes in Mathematics 326, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-540-46916-2, ISBN 978-3-540-06309-4, MR 0352107, Zbl 0256.14013
Roquette, Peter (1970), Analytic theory of elliptic functions over local fields, Hamburger Mathematische Einzelschriften (N.F.), Heft 1, Göttingen: Vandenhoeck & Ruprecht, MR 0260753, Zbl 0194.52002
Silverman, Joseph H. (1994). Advanced Topics in the Arithmetic of Elliptic Curves. Graduate Texts in Mathematics 151. Springer-Verlag. ISBN 0-387-94328-5. Zbl 0911.14015.
Tate, John (1995) [1959], "A review of non-Archimedean elliptic functions", in Coates, John; Yau, Shing-Tung, Elliptic curves, modular forms, & Fermat's last theorem (Hong Kong, 1993), Series in Number Theory I, Int. Press, Cambridge, MA, pp. 162–184, ISBN 978-1-57146-026-4, MR 1363501