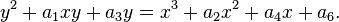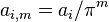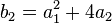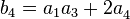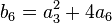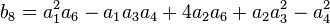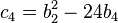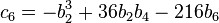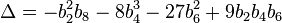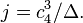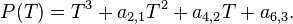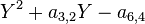Tate's algorithm
In the theory of elliptic curves, Tate's algorithm takes as input an integral model of an elliptic curve E over  , or more generally an algebraic number field, and a prime or prime ideal p. It returns the exponent fp of p in the conductor of E, the type of reduction at p, the local index
, or more generally an algebraic number field, and a prime or prime ideal p. It returns the exponent fp of p in the conductor of E, the type of reduction at p, the local index
where 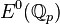 is the group of
is the group of 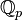 -points
whose reduction mod p is a non-singular point. Also, the algorithm determines whether or not the given integral model is minimal at p, and, if not, returns an integral model with integral coefficients for which the valuation at p of the discriminant is minimal.
-points
whose reduction mod p is a non-singular point. Also, the algorithm determines whether or not the given integral model is minimal at p, and, if not, returns an integral model with integral coefficients for which the valuation at p of the discriminant is minimal.
Tate's algorithm also gives the structure of the singular fibers given by the Kodaira symbol or Néron symbol, for which, see elliptic surfaces: in turn this determines the exponent fp of the conductor E.
Tate's algorithm can be greatly simplified if the characteristic of the residue class field is not 2 or 3; in this case the type and c and f can be read off from the valuations of j and Δ (defined below).
Tate's algorithm was introduced by John Tate (1975) as an improvement of the description of the Néron model of an elliptic curve by Néron (1964).
Notation
Assume that all the coefficients of the equation of the curve lie in a complete discrete valuation ring R with perfect residue field and maximal ideal generated by a prime π. The elliptic curve is given by the equation
Define:
The algorithm
- Step 1: If π does not divide Δ then the type is I0, f=0, c=1.
- Step 2. Otherwise, change coordinates so that π divides a3,a4,a6. If π does not divide b2 then the type is Iν, with ν =v(Δ), and f=1.
- Step 3. Otherwise, if π2 does not divide a6 then the type is II, c=1, and f=v(Δ);
- Step 4. Otherwise, if π3 does not divide b8 then the type is III, c=2, and f=v(Δ)−1;
- Step 5. Otherwise, if π3 does not divide b6 then the type is IV, c=3 or 1, and f=v(Δ)−2.
- Step 6. Otherwise, change coordinates so that π divides a1 and a2, π2 divides a3 and a4, and π3 divides a6. Let P be the polynomial
- If the congruence P(T)≡0 has 3 distinct roots then the type is I0*, f=v(Δ)−4, and c is 1+(number of roots of P in k).
- Step 7. If P has one single and one double root, then the type is Iν* for some ν>0, f=v(Δ)−4−ν, c=2 or 4: there is a "sub-algorithm" for dealing with this case.
- Step 8. If P has a triple root, change variables so the triple root is 0, so that π2 divides a2 and π3 divides a4, and π4 divides a6. If
- has distinct roots, the type is IV*, f=v(Δ)−6, and c is 3 if the roots are in k, 1 otherwise.
- Step 9. The equation above has a double root. Change variables so the double root is 0. Then π3 divides a3 and π5 divides a6. If π4 does not divide a4 then the type is III* and f=v(Δ)−7 and c = 2.
- Step 10. Otherwise if π6 does not divide a6 then the type is II* and f=v(Δ)−8 and c = 1.
- Step 11. Otherwise the equation is not minimal. Divide each an by πn and go back to step 1.
References
- Cremona, John (1997), Algorithms for modular elliptic curves (2nd ed.), Cambridge: Cambridge University Press, ISBN 0-521-59820-6, Zbl 0872.14041, retrieved 2007-12-20
- Laska, Michael (1982), "An Algorithm for Finding a Minimal Weierstrass Equation for an Elliptic Curve", Mathematics of Computation 38 (157): 257–260, doi:10.2307/2007483, JSTOR 2007483, Zbl 0493.14016
- Néron, André (1964), "Modèles minimaux des variétes abèliennes sur les corps locaux et globaux", Publications Mathématiques de l'IHÉS (in French) 21: 5–128, doi:10.1007/BF02684271, MR 0179172, Zbl 0132.41403
- Silverman, Joseph H. (1994), Advanced Topics in the Arithmetic of Elliptic Curves, Graduate Texts in Mathematics 151, Springer-Verlag, ISBN 0-387-94328-5, Zbl 0911.14015
- Tate, John (1975), "Algorithm for determining the type of a singular fiber in an elliptic pencil", in Birch, B.J.; W., Modular Functions of One Variable IV, Lecture Notes in Mathematics 476, Berlin / Heidelberg: Springer, pp. 33–52, doi:10.1007/BFb0097582, ISBN 978-3-540-07392-5, ISSN 1617-9692, MR 0393039, Zbl 1214.14020
![c_p=[E(\mathbb{Q}_p):E^0(\mathbb{Q}_p)],](../I/m/091763b0daf1bd9703ae17fbe7982c45.png)