Tangent space to a functor

In algebraic geometry, the tangent space to a functor generalizes the classical construction of a tangent space such as the Zariski tangent space. The construction is based on the following observation.[1] Let X be a scheme over a field k.

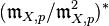To give a k[\epsilon]/(\epsilon)^2-point of X is the same thing as to give a k-rational point p of X (i.e., the residue field of p is k) together with an element of (\mathfrak{m}_{X, p}/\mathfrak{m}_{X, p}^2)^*; i.e., a tangent vector at p.

(To see this, use the fact that any local homomorphism \mathcal{O}_p \to k[\epsilon]/(\epsilon)^2 must be of the form

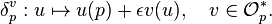\delta_p^v: u \mapsto u(p) + \epsilon v(u), \quad v \in \mathcal{O}_p^*.)

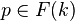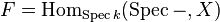Let F be a functor from the category of k-algebras to the category of sets. Then, for any k-point p \in F(k), the fiber of \pi: F(k[\epsilon]/(\epsilon)^2) \to F(k) over p is called the tangent space to F at p.[2] The tangent space may be given the structure of a vector space over k. If F is a scheme X over k (i.e., F = \operatorname{Hom}_{\operatorname{Spec}k}(\operatorname{Spec}-, X)), then each v as above may be identified with a derivation at p and this gives the identification of 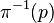\pi^{-1}(p) with the space of derivations at p and we recover the usual construction.

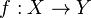The construction may be thought of as defining an analog of the tangent bundle in the following way.[3] Let T_X = X(k[\epsilon]/(\epsilon)^2). Then, for any morphism f: X \to Y of schemes over k, one sees 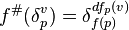f^{\#}(\delta_p^v) = \delta_{f(p)}^{df_p(v)}; this shows that the map 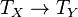T_X \to T_Y that f induces is precisely the differential of f under the above identification.

References

  1. ↑ Hartshorne 1977, Exercise II 2.8
  2. ↑ Eisenbud–Harris 1998, VI.1.3
  3. ↑ Borel 1991, AG 16.2