TITAN2D

TITAN2D
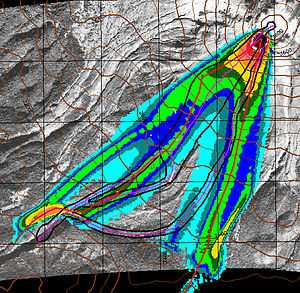Comparison of field observation and simulations for flows at Colima volcano
Developer(s) Geophysical Mass Flow Group
Stable release 2.0.0 / July 21, 2007
Operating system Unix-like
Type Geoflow Simulator
License NCSA Open Source License
Website GMFG

TITAN2D is a geoflow simulation software application, intended for geological researchers. It is distributed as free software.

Overview

TITAN2D is a free software application developed by the Geophysical Mass Flow Group at the State University of New York (SUNY) at Buffalo. TITAN2D was developed for the purpose of simulating granular flows (primarily geological mass flows such as debris avalanches and landslides) over digital elevation models (DEM)s of natural terrain. The code is designed to help scientists and civil protection authorities assess the risk of, and mitigate, hazards due to dry debris flows and avalanches. TITAN2D combines numerical simulations of a flow with digital elevation data of natural terrain supported through a Geographical Information System (GIS) interface such as GRASS.

TITAN2D is capable of multiprocessor runs. A Message Passing Interface (MPI) Application Programming Interface (API) allows for parallel computing on multiple processors, which effectively increases computational power, decreases computing time, and allows for the use of large data sets.

Adaptive gridding allows for the concentration of computing power on regions of special interest. Mesh refinement captures the complex flow features that occur at the leading edge of a flow, as well as locations where rapid changes in topography induce large mass and momentum fluxes. Mesh unrefinement is applied where solution values are relatively constant or small to further improve computational efficiency.

TITAN2D requires an initial volume and shape estimate for the starting material, a basal friction angle, and an internal friction angle for the simulated granular flow. The direct outputs of the program are dynamic representations of a flow's depth and momentum. Secondary or derived outputs include flow velocity, and such field-observable quantities as run-up height, deposit thickness, and inundation area.

Mathematical Model

The TITAN2D program is based upon a depth-averaged model for an incompressible Coulomb continuum, a “shallow-water” granular flow. The conservation equations for mass and momentum are solved with a Coulomb-type friction term for the interactions between the grains of the media and between the granular material and the basal surface. The resulting hyperbolic system of equations is solved using a parallel, adaptive mesh, Godunov scheme. The basic form of the depth-averaged governing equations appear as follows.

The depth-averaged conservation of mass is:

{\underbrace{\partial h \over \partial t}}_{ \begin{smallmatrix} \text{Change}\\ \text{in mass}\\ \text{over time} \end{smallmatrix}} + \underbrace{{\partial \overline{hu} \over \partial x} + {\partial \overline{hv} \over \partial y}}_{ \begin{smallmatrix} \text{Total spatial}\\ \text{variation of}\\ \text{x,y mass fluxes} \end{smallmatrix}} = 0

The depth-averaged x,y momentum balances are:

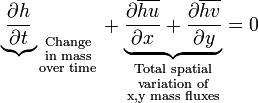
{\underbrace{\partial \overline{hu} \over \partial t}}_{ \begin{smallmatrix} \text{Change in}\\ \text{x mass flux}\\ \text{over time} \end{smallmatrix}} + \underbrace{{\partial \over \partial x} \left( \overline{hu^2}+{1 \over 2}{k_{ap}g_zh^2}\right) + {\partial \overline{huv} \over \partial y}}_{ \begin{smallmatrix} \text{Total spatial variation}\\ \text{of x,y momentum fluxes}\\ \text{in x-direction} \end{smallmatrix}} = \underbrace{-hk_{ap} \sgn \left({\partial u \over \partial y}\right){\partial hg_z \over \partial y}\sin \phi_{int}}_{ \begin{smallmatrix} \text{Dissipative internal}\\ \text{friction force}\\ \text{in x-direction} \end{smallmatrix}} - \underbrace{{u \over \sqrt{u^2+v^2}}\left[ g_zh \left(1+{u \over r_xg_x}\right) \right]\tan \phi_{bed}}_{ \begin{smallmatrix} \text{Dissipative basal}\\ \text{friction force}\\ \text{in x-direction} \end{smallmatrix}} + \underbrace{g_xh}_{ \begin{smallmatrix} \text{Driving}\\ \text{gravitational}\\ \text{force in}\\ \text{x-direction} \end{smallmatrix}}
{\underbrace{\partial \overline{hv} \over \partial t}}_{ \begin{smallmatrix} \text{Change in}\\ \text{y mass flux}\\ \text{over time} \end{smallmatrix}} + \underbrace{{\partial \overline{huv} \over \partial x} + {\partial \over \partial y} \left( \overline{hv^2}+{1 \over 2}{k_{ap}g_zh^2}\right)}_{ \begin{smallmatrix} \text{Total spatial variation}\\ \text{of x,y momentum fluxes}\\ \text{in y-direction} \end{smallmatrix}} = \underbrace{-hk_{ap} \sgn \left({\partial v \over \partial x}\right){\partial hg_z \over \partial x}\sin \phi_{int}}_{ \begin{smallmatrix} \text{Dissipative internal}\\ \text{friction force}\\ \text{in y-direction} \end{smallmatrix}} - \underbrace{{v \over \sqrt{u^2+v^2}}\left[ g_zh \left(1+{v \over r_yg_y}\right) \right]\tan \phi_{bed}}_{ \begin{smallmatrix} \text{Dissipative basal}\\ \text{friction force}\\ \text{in y-direction} \end{smallmatrix}} + \underbrace{g_yh}_{ \begin{smallmatrix} \text{Driving}\\ \text{gravitational}\\ \text{force in}\\ \text{y-direction} \end{smallmatrix}}


See also

External links

References