Szegő inequality
In functional analysis, a mathematical discipline, the Szegő inequality or Pólya–Szegő inequality, named after George Pólya and Gábor Szegő, states that if
and
then
where 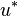 is the symmetric decreasing rearrangement of
is the symmetric decreasing rearrangement of 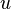 .
.
In functional analysis, a mathematical discipline, the Szegő inequality or Pólya–Szegő inequality, named after George Pólya and Gábor Szegő, states that if
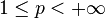
and
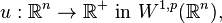
then
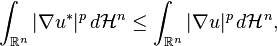
where 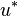 is the symmetric decreasing rearrangement of
is the symmetric decreasing rearrangement of 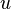 .
.