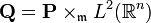Symplectic spinor bundle

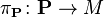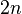In differential geometry, given a metaplectic structure \pi_{\mathbf P}\colon{\mathbf P}\to M\, on a 2n-dimensional symplectic manifold 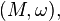(M, \omega),\, one defines the symplectic spinor bundle to be the Hilbert space bundle 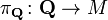\pi_{\mathbf Q}\colon{\mathbf Q}\to M\, associated to the metaplectic structure via the metaplectic representation. The metaplectic representation of the metaplectic group —the two-fold covering of the symplectic group— gives rise to an infinite rank vector bundle, this is the symplectic spinor construction due to Bertram Kostant.[1]

A section of the symplectic spinor bundle 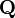{\mathbf Q}\, is called a symplectic spinor field.

Formal definition

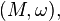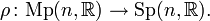
Let ({\mathbf P},F_{\mathbf P}) be a metaplectic structure on a symplectic manifold (M, \omega),\, that is, an equivariant lift of the symplectic frame bundle \pi_{\mathbf R}\colon{\mathbf R}\to M\, with respect to the double covering \rho\colon {\mathrm {Mp}}(n,{\mathbb R})\to {\mathrm {Sp}}(n,{\mathbb R}).\,

The symplectic spinor bundle 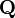{\mathbf Q}\, is defined [2] to be the Hilbert space bundle

{\mathbf Q}={\mathbf P}\times_{\mathfrak m}L^2({\mathbb R}^n)\,

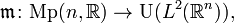associated to the metaplectic structure {\mathbf P} via the metaplectic representation {\mathfrak m}\colon {\mathrm {Mp}}(n,{\mathbb R})\to {\mathrm U}(L^2({\mathbb R}^n)),\, also called the Segal-Shale-Weil [3][4][5] representation of 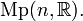{\mathrm {Mp}}(n,{\mathbb R}).\, Here, the notation 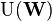{\mathrm U}({\mathbf W})\, denotes the group of unitary operators acting on a Hilbert space {\mathbf W}.\,

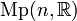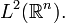The Segal-Shale-Weil representation [6] is an infinite dimensional unitary representation of the metaplectic group {\mathrm {Mp}}(n,{\mathbb R}) on the space of all complex valued square Lebesgue integrable functions L^2({\mathbb R}^n).\, Because of the infinite dimension, the Segal-Shale-Weil representation is not so easy to handle.

See also

Notes

  1. ↑ Kostant, B. (1974). "Symplectic Spinors". Symposia Mathematica (Academic Press) XIV: 139–152.
  2. ↑ Habermann, Katharina; Habermann, Lutz (2006), Introduction to Symplectic Dirac Operators, Springer-Verlag, ISBN 978-3-540-33420-0 page 37
  3. ↑ Segal, I.E (1962), Lectures at the 1960 Boulder Summer Seminar, AMS, Providence, RI
  4. ↑ Shale, D. (1962). "Linear symmetries of free boson fields". Trans. Amer. Math. Soc. 103: 149–167. doi:10.1090/s0002-9947-1962-0137504-6.
  5. ↑ Weil, A. (1964). "Sur certains groupes d’opérateurs unitaires". Acta Math. 111: 143–211. doi:10.1007/BF02391012.
  6. ↑ Kashiwara, M; Vergne, M. (1978). "On the Segal-Shale-Weil representation and harmonic polynomials". Inventiones Mathematicae 44: 1–47. doi:10.1007/BF01389900.

Books