Symplectic frame bundle
In symplectic geometry, the symplectic frame bundle[1] of a given symplectic manifold 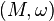 is the canonical principal
is the canonical principal 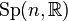 -subbundle
-subbundle  of the tangent frame bundle
of the tangent frame bundle 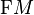 consisting of linear frames which are symplectic with respect to
consisting of linear frames which are symplectic with respect to 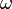 . In other words, an element of the symplectic frame bundle is a linear frame
. In other words, an element of the symplectic frame bundle is a linear frame 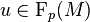 at point
at point 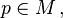 i.e. an ordered basis
i.e. an ordered basis 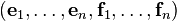 of tangent vectors at
of tangent vectors at 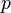 of the tangent vector space
of the tangent vector space 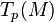 , satisfying
, satisfying
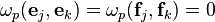 and
and 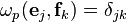
for 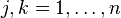 . For
. For 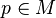 , each fiber
, each fiber 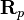 of the principal
of the principal 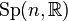 -bundle
-bundle  is the set of all symplectic bases of
is the set of all symplectic bases of 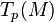 .
.
The symplectic frame bundle  , a subbundle of the tangent frame bundle
, a subbundle of the tangent frame bundle 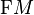 , is an example of reductive G-structure on the manifold
, is an example of reductive G-structure on the manifold 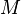 .
.
See also
- Metaplectic group
- Metaplectic structure
- Symplectic basis
- Symplectic structure
- Symplectic geometry
- Symplectic group
- Symplectic spinor bundle
Notes
Books
- Habermann, Katharina; Habermann, Lutz (2006), Introduction to Symplectic Dirac Operators, Springer-Verlag, ISBN 978-3-540-33420-0
- da Silva, A.C., Lectures on Symplectic Geometry, Springer (2001). ISBN 3-540-42195-5.
- Maurice de Gosson: Symplectic Geometry and Quantum Mechanics (2006) Birkhäuser Verlag, Basel ISBN 3-7643-7574-4.