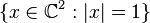Symplectic filling
In mathematics, a filling of a manifold X is a cobordism W between X and the empty set. More to the point, the n-dimensional topological manifold X is the boundary of an (n + 1)-dimensional manifold W. Perhaps the most active area of current research is when n = 3, where one may consider certain types of fillings.
There are many types of fillings, and a few examples of these types (within a probably limited perspective) follow.
- An oriented filling of any orientable manifold X is another manifold W such that the orientation of X is given by the boundary orientation of W, which is the one where the first basis vector of the tangent space at each point of the boundary is the one pointing directly out of W, with respect to a chosen Riemannian metric. Mathematicians call this orientation the outward normal first convention.
All the following cobordisms are oriented, with the orientation on W given by a symplectic structure. Let ξ denote the kernel of the contact form α.
- A weak symplectic filling of a contact manifold (X,ξ) is a symplectic manifold (W,ω) with
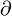 W = X such that
W = X such that 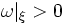 .
. - A strong symplectic filling of a contact manifold (X,ξ) is a symplectic manifold (W,ω) with
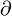 W = X such that ω is exact near the boundary (which is X) and α is a primitive for ω. That is, ω = dα in a neighborhood of the boundary
W = X such that ω is exact near the boundary (which is X) and α is a primitive for ω. That is, ω = dα in a neighborhood of the boundary 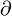 W = X.
W = X. - A Stein filling of a contact manifold (X,ξ) is a Stein manifold W which has X as its strictly pseudoconvex boundary and ξ is the set of complex tangencies to X – that is, those tangent planes to X that are complex with respect to the complex structure on W. The canonical example of this is the 3-sphere
- where the complex structure on
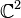 is multiplication by
is multiplication by 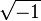 in each coordinate and W is the ball {x| < 1} bounded by that sphere.
in each coordinate and W is the ball {x| < 1} bounded by that sphere.
It is known that this list is strictly increasing in difficulty in the sense that there are examples of contact 3-manifolds with weak but no strong filling, and others that have strong but no Stein filling. Further, it can be shown that each type of filling is an example of the one preceding it, so that a Stein filling is a strong symplectic filling, for example. It used to be that one spoke of semi-fillings in this context, which means that X is one of possibly many boundary components of W, but it has been shown that any semi-filling can be modified to be a filling of the same type, of the same 3-manifold, in the symplectic world (Stein manifolds always have one boundary component).