Symplectic category
In mathematics, Weinstein's symplectic category is (roughly) a category whose objects are symplectic manifolds and whose morphisms are canonical relations, inclusions of Lagrangian submanifolds L into 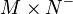 where the superscript minus means minus the given symplectic form (for example, the graph of a symplectomorphism; hence, minus). The notion was introduced by A. Weinstein, according to whom "Quantization problems[1] suggest that the category of symplectic manifolds and symplectomorphisms be augmented by the inclusion of canonical relations as morphisms." The composition of canonical relations is given by a fiber product.
where the superscript minus means minus the given symplectic form (for example, the graph of a symplectomorphism; hence, minus). The notion was introduced by A. Weinstein, according to whom "Quantization problems[1] suggest that the category of symplectic manifolds and symplectomorphisms be augmented by the inclusion of canonical relations as morphisms." The composition of canonical relations is given by a fiber product.
Strictly speaking, the symplectic category is not a well-defined category (since the composition may not be well-defined) without some transversality conditions.
References
- ↑ He means geometric quantization.
- Weinstein, Alan (2009). "Symplectic Categories". arXiv:0911.4133.
Further reading
- V. Guillemin and S. Sternberg, Some problems in integral geometry and some related problems in microlocal analysis, Amer. J. Math. 101, 915–955, 1979.