Symmetric probability distribution

In statistics, a symmetric probability distribution is a probability distribution—an assignment of probabilities to possible occurrences—which is unchanged when its probability density function or probability mass function is reflected around a vertical line at some value of the random variable represented by the distribution. This vertical line is the line of symmetry of the distribution. Thus the probability of being any given distance on one side of the value about which symmetry occurs is the same as the probability of being the same distance on the other side of that value.

Formal definition

A probability distribution is said to be symmetric if and only if there exists a value 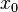$x_0$ such that

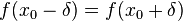f(x_0-\delta) = f(x_0+\delta)

for all real numbers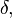

\delta ,

where f is the probability density function if the distribution is continuous or the probability mass function if the distribution is discrete.

Properties

The median and the mean (if it exists) of a symmetric distribution both occur at the point 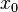$x_0$ about which the symmetry occurs.

If a symmetric distribution is unimodal, the mode coincides with the median.

All odd central moments of a symmetric distribution equal zero (if they exist), because in the calculation of such moments the negative terms arising from negative deviations from 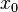$x_0$ exactly balance the positive terms arising from equal positive deviations from $x_0$ .

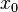Every measure of skewness equals zero for a symmetric distribution.

Probability density function

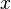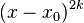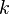Typically a symmetric continuous distribution's probability density function contains the index value $x$ only in the context of a term $(x-x_0)^{2k}$ where $k$ is some positive integer (usually 1). This quadratic or other even-powered term takes on the same value for 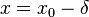$x=x_0 - \delta$ as for 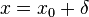$x=x_0 + \delta$ , giving symmetry about 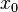$x_0$ . Sometimes the density function contains the term 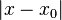$|x-x_0|$ , which also shows symmetry about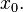 $x_0.$

Partial list of examples

The following distributions are symmetric for all parametrizations. (Many other distributions are symmetric for a particular parametrization.)

Probability distributions

Discrete univariate with finite support

Benford Bernoulli Beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support

beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval, e.g. [0,1]

Arcsine ARGUS Balding–Nichols Bates Beta Beta rectangular Irwin–Hall Kumaraswamy logit-normal Noncentral beta raised cosine Triangular U-quadratic uniform Wigner semicircle

[[List of probability distributions#Supported_on_semi-infinite_intervals.2C_usually_.5B0.2C.E2.88.9E.29|Continuous univariate supported on a semi-infinite interval, usually [0,∞)]]

Benini
Benktander 1st kind
Benktander 2nd kind
Beta prime
Burr
chi-squared
chi
Coxian
Dagum
Davis
EL
Erlang
exponential
F
folded normal
Flory-Schulz
Fréchet
Gamma
Gamma/Gompertz
generalized inverse Gaussian
Gompertz
half-logistic
half-normal
Hotelling's T-squared
hyper-Erlang
hyperexponential
hypoexponential
inverse chi-squared (scaled inverse chi-squared)
inverse Gaussian
inverse gamma
Kolmogorov
Lévy
log-Cauchy
log-Laplace
log-logistic
log-normal
matrix-exponential
Maxwell–Boltzmann
Maxwell–Jüttner
Mittag–Leffler
Nakagami
noncentral chi-squared
Pareto
phase-type
Poly-Weibull
Rayleigh
relativistic Breit–Wigner
Rice
Rosin–Rammler
shifted Gompertz
truncated normal
type-2 Gumbel
Weibull
Wilks' lambda

Continuous univariate supported on the whole real line (−∞, ∞)

Cauchy exponential power Fisher's z generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson SU Landau Laplace Linnik logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel Tracy–Widom variance-gamma Voigt

Continuous univariate with support whose type varies

generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential q-Weibull shifted log-logistic

Mixed continuous-discrete univariate distributions

rectified Gaussian

Multivariate (joint)

Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet Generalized Dirichlet multivariate normal Multivariate stable multivariate Student normal-scaled inverse gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional

Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular

Degenerate discrete degenerate Dirac delta function Singular Cantor

Families

Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped