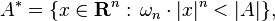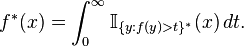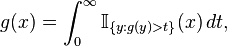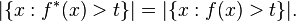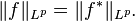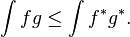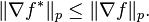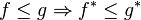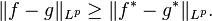Symmetric decreasing rearrangement
In mathematics, the symmetric decreasing rearrangement of a function is a function which is symmetric and decreasing, and whose level sets are of the same size as those of the original function.[1]
Definition for sets
Given a measurable set,  , in Rn one can obtain the symmetric rearrangement of
, in Rn one can obtain the symmetric rearrangement of  , called
, called 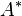 , by
, by
where 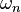 is the volume of the unit ball and where
is the volume of the unit ball and where 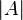 is the volume of
is the volume of  . Notice that this is just the ball centered at the origin whose volume is the same as that of the set
. Notice that this is just the ball centered at the origin whose volume is the same as that of the set  .
.
Definition for functions
The rearrangement of a non-negative, measurable function  whose level sets have finite measure is
whose level sets have finite measure is
In words, the value of 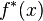 gives the height t for which the radius of the symmetric
rearrangement of
gives the height t for which the radius of the symmetric
rearrangement of 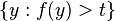 is equal to x. We have the following motivation for this definition. Because the identity
is equal to x. We have the following motivation for this definition. Because the identity
holds for any non-negative function 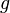 , the above definition is the unique definition that forces the identity
, the above definition is the unique definition that forces the identity 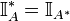 to hold.
to hold.
Properties
The function 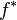 is a symmetric and decreasing function whose level sets have the same measure as the level sets of
is a symmetric and decreasing function whose level sets have the same measure as the level sets of  , i.e.
, i.e.
If  is a function in
is a function in 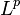 , then
, then
The Hardy–Littlewood inequality holds, i.e.
Further, the Szegő inequality holds. This says that if 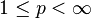 and if
and if 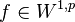 then
then
The symmetric decreasing rearrangement is order preserving and decreases 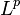 distance, i.e.
distance, i.e.
and
Applications
The Pólya–Szegő inequality yields, in the limit case, with 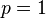 , the isoperimetric inequality. Also, one can use some relations with harmonic functions to prove the Rayleigh–Faber–Krahn inequality.
, the isoperimetric inequality. Also, one can use some relations with harmonic functions to prove the Rayleigh–Faber–Krahn inequality.
See also
- Isoperimetric inequality
- Layer cake representation
- Rayleigh–Faber–Krahn inequality
- Riesz rearrangement inequality
- Sobolev space
- Szegő inequality
References
- ↑ Lieb, Elliott; Loss, Michael (2001). Analysis. Graduate Studies in Mathematics 14 (2nd ed.). American Mathematical Society. ISBN 978-0821827833.