Suspension (dynamical systems)
Suspension is a construction passing from a map to a flow. Namely, let  be a metric space,
be a metric space, 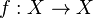 be a continuous map and
be a continuous map and 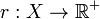 be a function (roof function or ceiling function) bounded away from 0. Consider the quotient space
be a function (roof function or ceiling function) bounded away from 0. Consider the quotient space
The suspension of 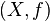 with roof function
with roof function  is the semiflow[1]
is the semiflow[1] 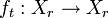 induced by the time-translation
induced by the time-translation 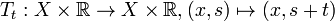 .
.
If 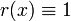 , then the quotient space is also called the mapping torus of
, then the quotient space is also called the mapping torus of 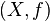 .
.
References
- ↑ M. Brin and G. Stuck, Introduction to Dynamical Systems, Cambridge University Press, 2002.