Suslin operation

In mathematics, the Suslin operation A is an operation that constructs a set from a collection of sets indexed by finite sequences of positive integers. The Suslin operation was introduced by Alexandrov (1916) and Suslin (1917). In Russia it is sometimes called the A-operation after Alexandrov. It is sometimes denoted by the symbol 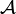$\mathcal A$ (a calligraphic capital letter A).

Definitions

Suppose we have Suslin scheme, in other words a function M from finite sequences of positive integers n₁,...,n_k to sets M_{n₁,...,n_k}. The result of the Suslin operation is the set

A(M) = ∪ (M_n₁ ∩ M_n₁,n₂ ∩ M_{n₁,n₂, n₃} ∩ ...)

where the union is taken over all infinite sequences n₁,...,n_k,...

If M is a family of subsets of a set X, then A(M) is the family of subsets of X obtained by applying the Suslin operation A to all collections as above where all the sets M_{n₁,...,n_k} are in M. The Suslin operation on collections of subsets of X has the property that A(A(M)) = A(M). The family A(M) is closed under taking countable unions or intersections, but is not in general closed under taking complements.

If M is the family of closed subsets of a topological space, then the elements of A(M) are called Suslin sets, or analytic sets if the space is a Polish space.

References

Aleksandrov, P.S. (1916), C.R. Acad. Sci. Paris 162: 323–325 Missing or empty |title= (help)
Hazewinkel, Michiel, ed. (2001), "A-operation", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Suslin, M.Ya. (1917), C.R. Acad. Sci. Paris 164: 88–91 Missing or empty |title= (help)